
【题目】如图,P,Q是方格纸中的两格点,请按要求画出以PQ为对角线的格点四边形.
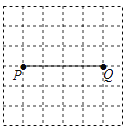
(1)在图1中画出一个面积最小的¨PAQB;
(2)在图2中画出一个四边形PCQD,使其是轴对称图形而不是中心对称图形,且另一条对角线CD由线段PQ以某一格点为旋转中心旋转得到.注:图1,图2在答题纸上.
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:初中数学 来源: 题型:
【题目】探索规律:观察下面由组成的图案和算式,解答问题:
1+3=4=22
1+3+5=9=32
1+3+5+7=16=42
1+3+5+7+9=25=52
(1)请计算 1+3+5+7+9+11;
(2)请计算 1+3+5+7+9+…+19;
(3)请计算 1+3+5+7+9+…+(2n﹣1);
(4)请用上述规律计算:21+23+25+…+99.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某高速公路养护小组乘车沿南北公路巡视维护,如果约定向北为正,向南为负,当天的行驶记录如下(单位:千米)+17,-9,+7,-15,+10,-8,+16.
(1)养护小组最后到达的地方在出发点的哪个方向?距离出发点多远?
(2)若汽车耗油量为0.3升/千米,则这次养护共耗油多少升?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)如图,在![]() 中,已知
中,已知![]() ,
,![]() ,
,![]() 与
与![]() 的平分线交于点
的平分线交于点![]() ,求证:
,求证:![]() 是等腰三角形.
是等腰三角形.
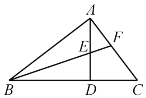
(2).阅读下列文字:我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到 ![]() .请解答下列问题:
.请解答下列问题:
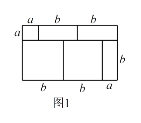
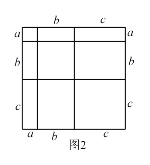
①.写出图2中所表示的数学等式;
②.利用(1)中所得到的结论,解决下面的问题:已知![]() ,
,![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简与求值
(1)求3x2+x+3(x2﹣![]() x)﹣(6x2+x)的值,其中x=﹣6.
x)﹣(6x2+x)的值,其中x=﹣6.
(2)先化简,再求值:5(3a2b﹣ab2)﹣4(﹣ab2+3a2b),其中|a+1|+(b﹣![]() )2=0
)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,由8个大小相等的小正方形构成的图案,它的四个顶点 E,F,G,H分别在矩形ABCD的边AB,BC,CD,DA上,若AB=4,BC=6,则DG的长是______.
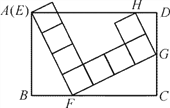
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线![]() 将这八个正方形分成面积相等的两部分,则该直线
将这八个正方形分成面积相等的两部分,则该直线![]() 的解析式为( )
的解析式为( )
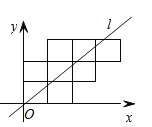
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和
矩形的三边AE,ED,DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的
距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数
关系![]() 且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com