
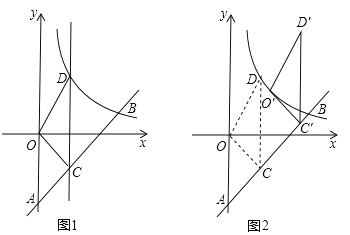
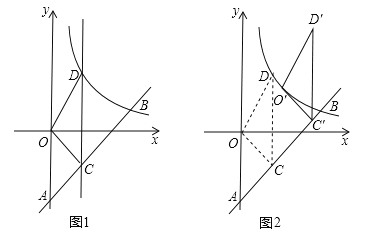
【题目】(2016江苏省镇江市) (2016镇江)如图1,一次函数y=kx﹣3(k≠0)的图象与y轴交于点A,与反比例函数![]() (x>0)的图象交于点B(4,b).
(x>0)的图象交于点B(4,b).
(1)b= ;k= ;
(2)点C是线段AB上的动点(于点A、B不重合),过点C且平行于y轴的直线l交这个反比例函数的图象于点D,求△OCD面积的最大值;
(3)将(2)中面积取得最大值的△OCD沿射线AB方向平移一定的距离,得到△O′C′D′,若点O的对应点O′落在该反比例函数图象上(如图2),则点D′的坐标是 .
【答案】(1)1,1;(2)![]() ;(3)D′(
;(3)D′(![]() ,
,![]() ).
).
【解析】试题(1)由点B的横坐标利用反比例函数图象上点的坐标特征即可求出b值,进而得出点B的坐标,再将点B的坐标代入一次函数解析式中即可求出k值;
(2)设C(m,m﹣3)(0<m<4),则D(m,![]() ),根据三角形的面积即可得出S△OCD关于m的函数关系式,通过配方即可得出△OCD面积的最大值;
),根据三角形的面积即可得出S△OCD关于m的函数关系式,通过配方即可得出△OCD面积的最大值;
(3)由(1)(2)可知一次函数的解析式以及点C、D的坐标,设点C′(a,a﹣3),根据平移的性质找出点O′、D′的坐标,由点O′在反比例函数图象上即可得出关于a的方程,解方程求出a的值,将其代入点D′的坐标中即可得出结论.
试题解析:解:(1)把B(4,b)代入![]() (x>0)中得:b=
(x>0)中得:b=![]() =1,∴B(4,1),把B(4,1)代入y=kx﹣3得:1=4k﹣3,解得:k=1,故答案为:1,1;
=1,∴B(4,1),把B(4,1)代入y=kx﹣3得:1=4k﹣3,解得:k=1,故答案为:1,1;
(2)设C(m,m﹣3)(0<m<4),则D(m,![]() ),∴S△OCD=
),∴S△OCD=![]() =
=![]() =
=![]() ,∵0<m<4,
,∵0<m<4,![]() <0,∴当m=
<0,∴当m=![]() 时,△OCD面积取最大值,最大值为
时,△OCD面积取最大值,最大值为![]() ;
;
(3)由(1)知一次函数的解析式为y=x﹣3,由(2)知C(![]() ,﹣
,﹣![]() )、D(
)、D(![]() ,
,![]() ).
).
设C′(a,a﹣3),则O′(a﹣![]() ,a﹣
,a﹣![]() ),D′(a,a+
),D′(a,a+![]() ),∵点O′在反比例函数
),∵点O′在反比例函数![]() (x>0)的图象上,∴
(x>0)的图象上,∴![]() ,解得:a=
,解得:a=![]() 或a=﹣
或a=﹣![]() (舍去),经检验a=
(舍去),经检验a=![]() 是方程
是方程![]() 的解,∴点D′的坐标是(
的解,∴点D′的坐标是(![]() ,
,![]() ).
).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
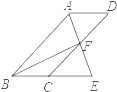
【题目】已知,如图,点P是平行四边形ABCD外一点,PE∥AB交BC于点E.PA、PD分别交BC于点M、N,点M是BE的中点.
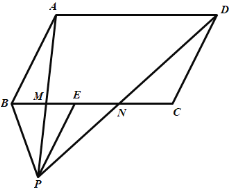
(1)求证:CN=EN;
(2)若平行四边形ABCD的面积为12,求△PMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在正方形ABCD中,对角线AC与BD相交于点O,AE,DF分别是∠OAD与∠ODC的平分线,AE的延长线与DF相交于点G,则下列结论:①AG⊥DF;②EF∥AB;③AB=AF;④AB=2EF.其中正确的结论是( )
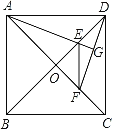
A.①②B.③④C.①②③D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形,∠BAD的角平分线AE交CD于点F,交BC的延长线于点E.
(1)求证:BE=CD;
(2)连接BF,若BF⊥AE,∠BEA=60°,AB=4,求平行四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小轩从如图所示的二次函数y=ax2+bx+c(a≠0)的图象中,观察得出了下面五条信息:
①ab>0;②a+b+c<0;③b+2c>0;④a﹣2b+4c>0;⑤![]() .
.
你认为其中正确信息的个数有
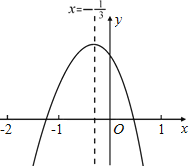
A.2个 B.3个 C.4个 D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
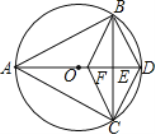
【题目】如图,已知△ABC内接于⊙O,且AB=AC,直径AD交BC于点E,F是OE上的一点,CF![]() BD.
BD.
(1)求证:BE=CE;
(2)试判断四边形BFCD的形状,并说明理由;
(3)若BC=6,AD=10,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
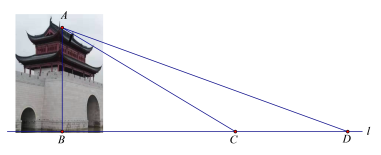
【题目】水城门位于淀浦河和漕港河三叉口,是环城水系公园淀浦河梦蝶岛区域重要的标志性景观.在课外实践活动中,某校九年级数学兴趣小组决定测量该水城门的高.他们的操作方法如下:如图,先在D处测得点A的仰角为20°,再往水城门的方向前进13米至C处,测得点A的仰角为31°(点D、C、B在一直线上),求该水城门AB的高.(精确到0.1米)
(参考数据:sin20°≈0.34,cos20°≈0.94,tan20°≈0.36,sin31°≈0.52,cos31°≈0.86,tan31°≈0.60)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,lA、lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距_____千米.
(2)走了一段路后,自行车发生故障进行修理,所用的时间是____小时.
(3)B出发后_____小时与A相遇.
(4)求出A行走的路程S与时间t的函数关系式.(写出计算过程)
(5)请通过计算说明:若B的自行车不发生故障,保持出发时的速度前进,何时与A相遇?

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com