
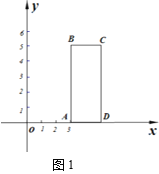
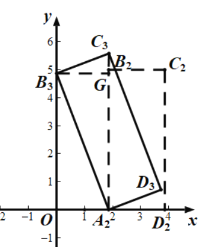
°æƒø°ø»ÁÕº1£¨‘⁄æÿ–ŒABCD÷–£¨AB£Ω5£¨AD£Ω2£¨∞—À¸∑≈‘⁄x÷·µƒ’˝∞Î÷·…œ£¨AD”Îx÷·÷ÿ∫œ«“µ„A◊¯±ÍŒ™(3£¨0)£Æ
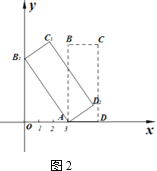
£®1£©»Ù“‘µ„AŒ™–˝◊™÷––ƒ£¨Ω´æÿ–ŒABCDƒÊ ±’Ζ˝◊™£¨ πµ„B¬‰µΩy÷·…œµƒµ„B1¥¶£¨µ√µΩæÿ–ŒAB1C1D1£¨»ÁÕº2£¨«Ûµ„B1£¨C1£¨D1µƒ◊¯±Í£Æ
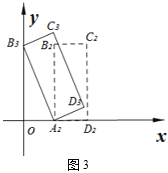
£®2£©»ÙΩ´æÿ–ŒABCDœÚ◊Û∆Ω“∆“ª∂Œæý¿Î∫Ûµ√µΩæÿ–ŒA2B2C2D2£¨»ÁÕº3£¨‘ŸΩ´À¸“‘A2Œ™–˝◊™÷––ƒƒÊ ±’Ζ˝◊™£¨ πµ„B2¬‰µΩy÷·…œµƒµ„B3¥¶£Æ¥À ±µ„C3«°∫√¬‰‘⁄µ„A2µƒ’˝…œ∑Ωµ√µΩæÿ–ŒA2B3C3D3£¨«Û∆Ω“∆µƒæý¿Î≤¢–¥≥ˆC3µƒ◊¯±Í£Æ
°æ¥∞∏°ø£®1£©B1(0£¨4)£¨![]() £¨D1(4.6£¨1.2)£ª£®2£©∆Ω“∆µƒæý¿Î£∫
£¨D1(4.6£¨1.2)£ª£®2£©∆Ω“∆µƒæý¿Î£∫![]() £¨C3(
£¨C3(![]() £¨
£¨![]() )£Æ
)£Æ
°æΩ‚Œˆ°ø
£®1£©œ»«Û≥ˆB1µƒ◊¯±ÍŒ™(0£¨4)£¨π˝D1◊˜D1E°Õx÷·”⁄E£¨¿˚”√Rt°˜AOB1°◊Rt°˜D1EA«Û≥ˆED1£Ω1.2£¨EA£Ω1.6£¨Ω¯∂¯µ√≥ˆD1µƒ◊¯±Í£ªπ˝µ„C1◊˜C1F°Õy÷·”⁄F£¨¿˚”√Rt°˜B1C1F°◊Rt°˜AB1O£¨µ√≥ˆ°œC1B1F£Ω°œB1AO£¨¿˚”√»˝Ω«∫Ø ˝«Û≥ˆ![]() £¨
£¨![]() µƒ÷µ£¨Ω¯∂¯µ√≥ˆ
µƒ÷µ£¨Ω¯∂¯µ√≥ˆ![]() µƒ◊¯±Í£ª
µƒ◊¯±Í£ª
£®2£©¡¨Ω”B2C3£¨π˝µ„B3◊˜B3G°ÕA2C3”⁄G£¨‘⁄Rt°˜A2B3C3÷–¿˚”√π¥π…∂®¿Ì«Û≥ˆA2C3µƒ÷µ£¨¿˚”√µ»√ʪ˝∑®«Û≥ˆ![]() µƒ÷µ£¨¥”∂¯µ√≥ˆC3µƒ◊¯±Í£Æ
µƒ÷µ£¨¥”∂¯µ√≥ˆC3µƒ◊¯±Í£Æ
Ω‚£∫£®1£©°þA(3£¨0)£¨°ýOA£Ω3£¨
°þAB£Ω5£¨°ý”…–˝◊™µƒ–‘÷ ø…÷™AB1£ΩAB£Ω5£¨
‘⁄Rt°˜AOB1÷–£¨”…π¥π…∂®¿Ìø…µ√£∫
OB1£Ω![]() 4£¨
4£¨
°ýB1µƒ◊¯±ÍŒ™(0£¨4)£¨
»Áœ¬Õº£¨π˝D1◊˜D1E°Õx÷·”⁄E£¨
°þÀƒ±þ–ŒAB1C1D1 «æÿ–Œ£¨
°ý°œB1AD1£Ω90°„£¨°ý°œOAB1£´°œEAD1£Ω90°„£¨
”÷°þ°œOAB1£´°œOB1A£Ω90°„£¨
°ý°œEAD1£Ω°œOB1A£¨
”÷°þ°œAOB1£Ω°œAED1£Ω90°„£¨
°ýRt°˜AOB1°◊Rt°˜D1EA£¨
°ý![]() £¨
£¨
”…–˝◊™–‘÷ ø…÷™£¨AD1£ΩAD£Ω2£¨
°ý![]() £¨
£¨
°ýED1£Ω1.2£¨EA£Ω1.6£¨
°ýOE£ΩOA£´AE£Ω3£´1.6£Ω4.6£¨
°ýD1(4.6£¨1.2)£¨
π˝µ„C1◊˜C1F°Õy÷·”⁄F£¨
Õ¨¿Ìø…µ√£¨°ýRt°˜B1C1F°◊Rt°˜AB1O£¨
°ý°œC1B1F£Ω°œB1AO£¨
°þ![]()
°ý![]() £¨∂¯
£¨∂¯![]() £¨
£¨
°ý![]() £¨Ω‚µ√
£¨Ω‚µ√![]() £¨
£¨
°ý![]() ‘Ú
‘Ú![]() Ω‚µ√
Ω‚µ√![]()
°ý![]()
°ý![]() £Æ
£Æ
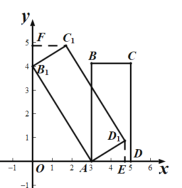
£®2£©¡¨Ω”B2C3£¨π˝µ„B3◊˜B3G°ÕA2C3”⁄G£¨
‘⁄Rt°˜A2B3C3÷–£¨A2B3£ΩAB£Ω5£¨B3C3£ΩBC£Ω2£¨
°ýA2C3£Ω![]() £¨
£¨
”÷°þ![]() £¨
£¨
°ý![]() £¨
£¨
º¥![]() °ý
°ý![]() £¨
£¨
°ý![]()
“Ú¥ÀœÚ◊Û∆Ω“∆µƒæý¿ÎŒ™£∫![]() £¨
£¨
°þOA2£Ω![]() £¨A2C3£Ω
£¨A2C3£Ω![]()
°ýµ„C3µƒ◊¯±ÍŒ™(![]() £¨
£¨![]() )£Æ
)£Æ



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
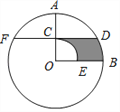
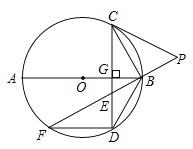
°æƒø°ø»ÁÕº£¨‘⁄°—O÷–£¨∞Îæ∂OA°ÕOB£¨π˝OAµƒ÷–µ„C◊˜FD°ŒOBΩª°—O”⁄D°¢F¡Ωµ„£¨«“CD£Ω![]() £¨“‘OŒ™‘≤–ƒ£¨OCŒ™∞Îæ∂◊˜
£¨“‘OŒ™‘≤–ƒ£¨OCŒ™∞Îæ∂◊˜![]() £¨ΩªOB”⁄Eµ„£Æ‘ÚÕº÷–“ı”∞≤ø∑÷µƒ√ʪ˝Œ™______________£Æ
£¨ΩªOB”⁄Eµ„£Æ‘ÚÕº÷–“ı”∞≤ø∑÷µƒ√ʪ˝Œ™______________£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨∂˛¥Œ∫Ø ˝![]() µƒÕºœÛæ≠π˝µ„A£®
µƒÕºœÛæ≠π˝µ„A£®![]() £¨0£©£¨∆‰∂‘≥∆÷·Œ™÷±œþ
£¨0£©£¨∆‰∂‘≥∆÷·Œ™÷±œþ![]() £¨‘Úœ¬¡–Ω·¬€¥ÌŒÛµƒ «£® £©
£¨‘Úœ¬¡–Ω·¬€¥ÌŒÛµƒ «£® £©
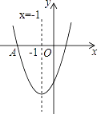
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø–°–˘¥”»ÁÕºÀ˘ 浃∂˛¥Œ∫Ø ˝y=ax2+bx+c£®a°Ÿ0£©µƒÕºœÛ÷–£¨π€≤ϵ√≥ˆ¡Àœ¬√ÊŒÂÃı–≈œ¢£∫
¢Ÿab£æ0£ª¢⁄a+b+c£º0£ª¢€b+2c£æ0£ª¢Ða©Å2b+4c£æ0£ª¢ð![]() £Æ
£Æ
ƒ„»œŒ™∆‰÷–’˝»∑–≈œ¢µƒ∏ˆ ˝”–
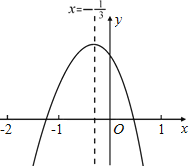
A£Æ2∏ˆ B£Æ3∏ˆ C£Æ4∏ˆ D£Æ5∏ˆ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
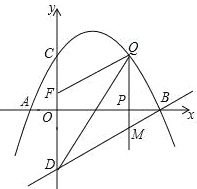
°æƒø°ø»ÁÕº£¨“—÷™≈◊ŒÔœþæ≠π˝µ„A£®©Å1£¨0£©£¨B£®4£¨0£©£¨C£®0£¨2£©»˝µ„£¨µ„D”ε„Cπÿ”⁄![]() ÷·∂‘≥∆£¨µ„P «
÷·∂‘≥∆£¨µ„P «![]() ÷·…œµƒ“ª∏ˆ∂ص„£¨…˵„Pµƒ◊¯±ÍŒ™£®
÷·…œµƒ“ª∏ˆ∂ص„£¨…˵„Pµƒ◊¯±ÍŒ™£®![]() £¨0£©£¨π˝µ„P◊ˆ
£¨0£©£¨π˝µ„P◊ˆ![]() ÷·µƒ¥πœþlΩª≈◊ŒÔœþ”⁄µ„Q£¨Ωª÷±œþBD”⁄µ„M£Æ
÷·µƒ¥πœþlΩª≈◊ŒÔœþ”⁄µ„Q£¨Ωª÷±œþBD”⁄µ„M£Æ
£®1£©«Û∏√≈◊ŒÔœþÀ˘±Ì 浃∂˛¥Œ∫Ø ˝µƒ±Ì¥Ô Ω£ª
£®2£©µ„P‘⁄œþ∂ŒAB‘À∂Øπ˝≥Ã÷–£¨ «∑ҥʑ⁄µ„Q£¨ πµ√°˜BOD°◊°˜QBM£ø»Ù¥Ê‘⁄£¨«Û≥ˆµ„Qµƒ◊¯±Í£ª»Ù≤ª¥Ê‘⁄£¨«ÎÀµ√˜¿Ì”…£Æ
£®3£©“—÷™µ„F£®0£¨![]() £©£¨µ±µ„P‘⁄
£©£¨µ±µ„P‘⁄![]() ÷·…œ‘À∂Ø ±£¨ ‘«Û
÷·…œ‘À∂Ø ±£¨ ‘«Û![]() Œ™∫Œ÷µ ±£¨“‘D£¨M£¨Q£¨FŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£ø
Œ™∫Œ÷µ ±£¨“‘D£¨M£¨Q£¨FŒ™∂•µ„µƒÀƒ±þ–Œ «∆Ω––Àƒ±þ–Œ£ø
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
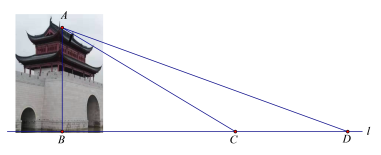
°æƒø°øÀÆ≥«√≈Œª”⁄µÌ∆÷∫”∫Õ‰Ó∏€∫”»˝≤Êø⁄£¨ «ª∑≥«ÀÆœµπ´‘∞µÌ∆÷∫”√Œµ˚µ∫«¯”Ú÷ÿ“™µƒ±Í÷æ–‘æ∞π€£Æ‘⁄øŒÕ‚ µº˘ªÓ∂Ø÷–£¨ƒ≥–£æ≈ƒÍº∂ ˝—ß–À»§–°◊Èæˆ∂®≤‚¡ø∏√ÀÆ≥«√≈µƒ∏þ£ÆÀ˚√«µƒ≤Ÿ◊˜∑Ω∑®»Áœ¬£∫»ÁÕº£¨œ»‘⁄D¥¶≤‚µ√µ„Aµƒ—ˆΩ«Œ™20°„£¨‘ŸÕ˘ÀÆ≥«√≈µƒ∑ΩœÚ«∞Ω¯13√◊÷¡C¥¶£¨≤‚µ√µ„Aµƒ—ˆΩ«Œ™31°„£®µ„D°¢C°¢B‘⁄“ª÷±œþ…œ£©£¨«Û∏√ÀÆ≥«√≈ABµƒ∏þ£Æ£®æ´»∑µΩ0.1√◊£©
£®≤Œøº ˝æð£∫sin20°„°÷0.34£¨cos20°„°÷0.94£¨tan20°„°÷0.36£¨sin31°„°÷0.52£¨cos31°„°÷0.86£¨tan31°„°÷0.60£©
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
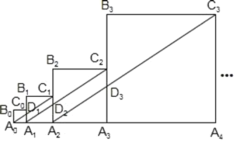
°æƒø°ø»ÁÕº£¨’˝∑Ω–ŒA0B0C0A1µƒ±þ≥§Œ™1£¨’˝∑Ω–ŒA1B1C1A2µƒ±þ≥§Œ™2£¨’˝∑Ω–ŒA2B2C2A3µƒ±þ≥§Œ™4£¨’˝∑Ω–ŒA3B3C3A4µƒ±þ≥§Œ™8°≠°≠“¿¥Àπʬ…ºÃ–¯◊˜’˝∑Ω–ŒAnBnnAn+1£¨«“µ„A0£¨A1£¨A2£¨A3£¨°≠£¨An+1‘⁄Õ¨“ªÃı÷±œþ…œ£¨¡¨Ω”A0C1ΩªA1B1”⁄µ„D1£¨¡¨Ω”A1C2ΩªA2B2”⁄µ„D2£¨¡¨Ω”A2C3ΩªA3B3”⁄µ„D3°≠°≠º«Àƒ±þ–ŒA0B0C0D1µƒ√ʪ˝Œ™S1£¨Àƒ±þ–ŒA1B1C1D2µƒ√ʪ˝Œ™S2£¨Àƒ±þ–ŒA2B2C2D3µƒ√ʪ˝Œ™S3°≠°≠Àƒ±þ–ŒAn©Å1Bn©Å1Cn©Å1Dnµƒ√ʪ˝Œ™Sn£¨‘ÚS2019£Ω_____£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
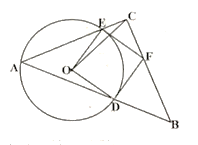
°æƒø°ø»ÁÕº£¨µ»—¸![]() µƒ“ª∏ˆ»ÒΩ«∂•µ„
µƒ“ª∏ˆ»ÒΩ«∂•µ„![]() «
«![]() …œµƒ“ª∏ˆ∂ص„£¨
…œµƒ“ª∏ˆ∂ص„£¨![]() £¨—¸
£¨—¸![]() ”Ζ±±þ
”Ζ±±þ![]() ∑÷±Ωª
∑÷±Ωª![]() ”⁄µ„
”⁄µ„![]() £¨∑÷±π˝µ„
£¨∑÷±π˝µ„![]() ◊˜
◊˜![]() µƒ«–œþΩª”⁄µ„
µƒ«–œþΩª”⁄µ„![]() £¨«“µ„
£¨«“µ„![]() «°∫√ «—¸
«°∫√ «—¸![]() …œµƒµ„£¨¡¨Ω”
…œµƒµ„£¨¡¨Ω”![]() £¨»Ù
£¨»Ù![]() µƒ∞Îæ∂Œ™4£¨‘Ú
µƒ∞Îæ∂Œ™4£¨‘Ú![]() µƒ◊Ó¥Û÷µŒ™£∫£® £©
µƒ◊Ó¥Û÷µŒ™£∫£® £©
A.![]() B.
B.![]() C.6D.8
C.6D.8
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫≥ı÷– ˝—ß ¿¥‘¥£∫ –գ∫
°æƒø°ø»ÁÕº£¨![]() Œ™
Œ™![]() µƒ÷±æ∂£¨
µƒ÷±æ∂£¨![]() ”⁄µ„
”⁄µ„![]() £¨
£¨![]() «
«![]() …œ“ªµ„£¨«“
…œ“ªµ„£¨«“![]() £¨—”≥§
£¨—”≥§![]() ÷¡µ„
÷¡µ„![]() £¨¡¨Ω”
£¨¡¨Ω”![]() £¨ π
£¨ π![]() £¨—”≥§
£¨—”≥§![]() ”Î
”Î![]() Ωª”⁄µ„
Ωª”⁄µ„![]() £¨¡¨Ω·
£¨¡¨Ω·![]() £¨
£¨![]() £Æ
£Æ
£®1£©¡¨Ω·![]() £¨«Û÷§£∫
£¨«Û÷§£∫![]() £ª
£ª
£®2£©«Û÷§£∫![]() «
«![]() µƒ«–œþ£ª
µƒ«–œþ£ª
£®3£©»Ù![]() £¨
£¨![]() £¨«Û
£¨«Û![]() µƒ÷µ£Æ
µƒ÷µ£Æ
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com