
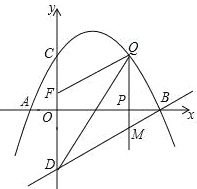
����Ŀ����ͼ����֪�����߾�����A����1��0����B��4��0����C��0��2�����㣬��D���C����![]() ��Գƣ���P��
��Գƣ���P��![]() ���ϵ�һ�����㣬���P������Ϊ��
���ϵ�һ�����㣬���P������Ϊ��![]() ��0��������P��
��0��������P��![]() ��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
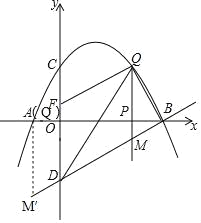
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ����BOD�ס�QBM�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����֪��F��0��![]() ��������P��
��������P��![]() �����˶�ʱ������
�����˶�ʱ������![]() Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
���𰸡���1��![]() ����2�����ڣ�
����2�����ڣ�![]() ����3��-1��3��
����3��-1��3��![]() ��
��![]()
��������
��1�����ô���ϵ������⼴�ɣ�
��2����������ͼ��֪��DOB�ס�MBQ����MBQ�ס�QPB����BOD�ס�QPB������![]() ���ɵ������ɵ�
���ɵ������ɵ�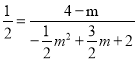 ����֮���ɵô�ʱmֵ��
����֮���ɵô�ʱmֵ��
��3�������ô���ϵ�������ֱ��BD�Ľ���ʽ�������õ���Q��M�����꣬����QM��DF���ı���DMQF��ƽ���ı���֪QM=DF���ݴ��г�����m�ķ��̣���֮����.
��1���������߹���A����1��0����B��4��0���������ʽΪy=a��x+1����x��4��������C��0��2�����룬�ã���4a=2����ã�a=��![]() ��
��
�������߽���ʽΪy=��![]() ��x+1����x��4��=��
��x+1����x��4��=��![]() ��
��
��2������ ��������
�ߡ�MBQ=90���MBP+��PBQ=90
�ߡ�MPB=��BPQ=90��
���MBQ+��BMP=90��
���PBQ=��BMP��
����MBQ�ס�QPB��
�ߡ�DOB�ס�MBQ��
���BOD�ס�QPB��
��![]() ����
����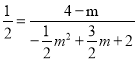 ��
��
��ã�m1=3��m2=4��
��m=4ʱ����P��Q��M�����B�غϣ����ܹ��������Σ���ȥ��
��m=3����Q��������3��2����
��3��������֪��D����Ϊ��0����2������ֱ��BD����ʽΪy=kx+b��
��B��4��0����D��0����2�����룬�ã�![]() ����ã�
����ã�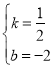 ��
��
��ֱ��BD����ʽΪy=![]() x��2����QM��x�ᣬP��m��0����
x��2����QM��x�ᣬP��m��0����
��Q��m��![]() ����M��m��
����M��m��![]() m��
m��
��QM=|![]() ����
����![]() m��2��|=|��
m��2��|=|��![]() m2+m+4|��
m2+m+4|��
��F��0��![]() ����D��0����2������DF=
����D��0����2������DF=![]() ����QM��DF��
����QM��DF��
�൱|��![]() m2+m+4|=
m2+m+4|=![]() ʱ���ı���DMQF��ƽ���ı��Σ���ã�m=��1��m=3��
ʱ���ı���DMQF��ƽ���ı��Σ���ã�m=��1��m=3��![]()
��m=��1��m=3��![]() ʱ���ı���DMQF��ƽ���ı��Σ�
ʱ���ı���DMQF��ƽ���ı��Σ�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪OA�ǡ�O�İ뾶��OA=1����P��OA��һ���㣬��P����BC��OA������AB��AC��
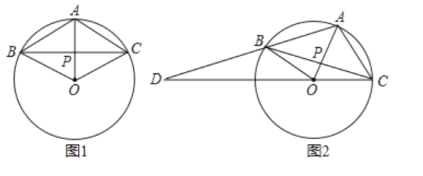
��1����ͼ1����PΪOA�е㣬��AC=______����ACB=_______����
��2����ͼ2�����ƶ���P��ʹAB��CO���ӳ��߽��ڵ�D������AOC�����ΪS1����BOD�����ΪS2����AOD�����ΪS3��������![]() ����
����![]() ��ֵ��
��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
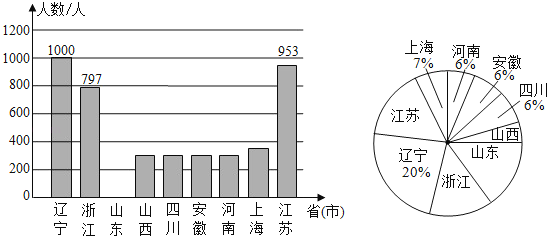
����Ŀ��2020�괺��ǰϦ������״�������������������������ؾ���ʹ����ȫ�����س�Ԯ�人��ҽ�������ߣ�����ҽ�����ĵ�ʹ���뵣������С�ң�Ϊ��ң����Լ���רҵ֪ʶ��Ѫ��֮��������ȫ��Ό������ĸ������ǣ�������2��9�յ���ȫ������ʡ�г�Ԯ�人ҽ�������ߵ�����ͳ��ͼ������������
�����������⣺
��1��������ʡ��2��9�յ����Ԯ�人��ҽ�������ߵ�������Ϊ�� ���ˣ�
���뽫����ͳ��ͼ����������
��2�����������ͳ��ͼ�С�ɽ��������Ӧ���ε�Բ�ĽǵĶ�����
��3������ɽ����Ԯ�人��ҽ���������У���5�˱���ȥ��֢������ҽ������ҽ���������У����ӱ�����5�����������2�ˣ���ͬʱ������ҽ������ҽ���ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
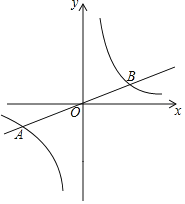
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У���֪����������y��![]() x��ͼ���뷴��������y��
x��ͼ���뷴��������y��![]() ��ͼ���ڵ�A��a����2����B���㣮
��ͼ���ڵ�A��a����2����B���㣮
��1�������������ı���ʽ�� ������B������Ϊ�� ����
��2������ʽ![]() x��
x��![]() ��0�Ľ⼯Ϊ�� ����
��0�Ľ⼯Ϊ�� ����
��3��P�ǵ�һ�����ڷ�����������ͼ����һ�㣬����P��y���ƽ���ߣ���ֱ��AB�ڵ�C������PO������POC�����Ϊ3�����P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ӡ�����ӽ���������������ܵ����㷺��ע������ijУ�͡��л��Ļ��Ҵ��С����ط�Ϸ����У����ϲ�����������������飬���ռ�����Ϣ����ͳ�ƣ����������������в�������ͳ��ͼ���������ͳ��ͼ���ṩ����Ϣ����������⣺
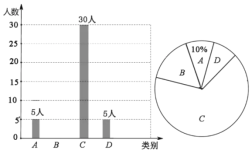
ͼ��A��ʾ����ϲ������B��ʾ��ϲ������C��ʾ��һ�㡱��D��ʾ����ϲ����
��1�����������������________�ˣ�����ͳ��ͼ��C��������Ӧ������Բ�ĽǵĶ���Ϊ______��
��2����ȫ����ͳ��ͼ��
��3������У����ѧ��1800�ˣ���������������������Ƹ�Уѧ����D����______�ˣ�
��4���ڳ�ȡ��A��5���У��պ���3��Ů��2�����������������ȡ����ͬѧ��������ɫ��������ͼ���б���������鵽������ѧ���Ա���ͬ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
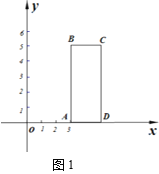
����Ŀ����ͼ1���ھ���ABCD�У�AB��5��AD��2����������x����������ϣ�AD��x���غ��ҵ�A����Ϊ(3��0)��
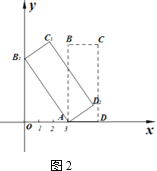
��1�����Ե�AΪ��ת���ģ�������ABCD��ʱ����ת��ʹ��B�䵽y���ϵĵ�B1�����õ�����AB1C1D1����ͼ2�����B1��C1��D1�����꣮
��2����������ABCD����ƽ��һ�ξ����õ�����A2B2C2D2����ͼ3���ٽ�����A2Ϊ��ת������ʱ����ת��ʹ��B2�䵽y���ϵĵ�B3������ʱ��C3ǡ�����ڵ�A2�����Ϸ��õ�����A2B3C3D3����ƽ�Ƶľ��벢д��C3�����꣮
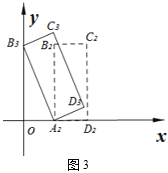
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����꼶��1�����о���ѧϰС��Ϊ�о�ȫУͬѧ�����Ķ��������ȫУ��������˲���ͬѧ�����ʾ����飬ͳ��ͬѧ��һ�����Ķ�������������������������µ�ͳ��ͼ1��ͼ2�������ͼ�������Ϣ������������⣺
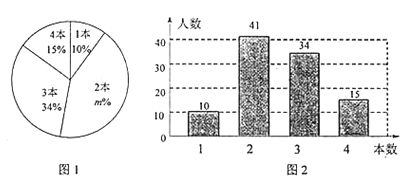
����ͼ1��![]() ��ֵΪ____________������____________��ͬѧ�����ʾ����飻
��ֵΪ____________������____________��ͬѧ�����ʾ����飻
������ͳ�Ƶ��������ݵ�ƽ��������������λ����
����ȫУ����ѧ��1500�ˣ������������ݣ����Ƹ�Уѧ��һ�����Ķ�2�������������ԼΪ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���![]() ��ͼ������ʽ�����̽����̽���������£��벹��������
��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���![]() ��ȡֵ��Χ��ȫ��ʵ����
��ȡֵ��Χ��ȫ��ʵ����![]() ��
��![]() �ļ����Ӧֵ�б����£�
�ļ����Ӧֵ�б����£�
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
����![]() ����������
����������
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�������˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
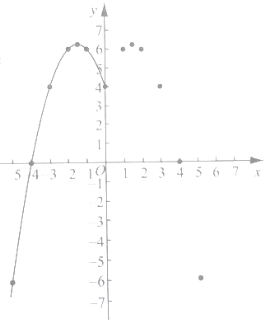
��3���۲캯��ͼ��д���������������ʣ�
��4��ֱ��![]() ����
����![]() ��������
��������![]() �ķ���
�ķ���![]() ��
��![]() ������ȵ�ʵ��������
������ȵ�ʵ��������![]() ��ȡֵ��ΧΪ����������
��ȡֵ��ΧΪ����������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У���C��90����AC��8 cm��BC��6 cm.����P���߶�AC����5 cm/s���ٶȴӵ�A�˶�����C.����P��PD��AB�ڵ�D����PDΪһ������������PDEF������ʹDE��AD.���P���˶�ʱ��Ϊt s������PDEF����ABC�ص�����ͼ���ܳ�Ϊy cm��
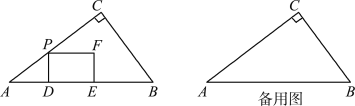
(1)����F���ڱ�BC��ʱ����t��ֵ��
(2)��y��t֮��ĺ�����ϵʽ��
(3)������PDEF��������߶�BCƽ��ʱ��t��______��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com