
【题目】如图,在△ABC中,∠C=90°,AC=8 cm,BC=6 cm.动点P在线段AC上以5 cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,以PD为一边向右作矩形PDEF,并且使DE=AD.设点P的运动时间为t s,矩形PDEF和△ABC重叠部分图形周长为y cm.
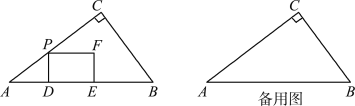
(1)当点F落在边BC上时,求t的值;
(2)求y与t之间的函数关系式;
(3)当矩形PDEF的面积被线段BC平分时,t=______.
【答案】(1) t=![]() ;(2)①y=14t;②y=
;(2)①y=14t;②y=![]() t+
t+![]() ;③y=-
;③y=-![]() t+20;(3)
t+20;(3) ![]() .
.
【解析】
(1)如图1,由题意得出AB=10、AP=5t、PC=85t,利用△APD∽△ABC求得AD=4t、PD=3t,据此知PF=DE=AD=4t,由△CPF∽△CAB得![]() ,据此可得答案;
,据此可得答案;
(2)分0<t≤![]() ,
,![]() <t≤
<t≤![]() 和
和![]() ≤t≤
≤t≤![]() 这三种情况,利用相似三角形的判定与性质求出重合部分图形的各边长度,从而得解;
这三种情况,利用相似三角形的判定与性质求出重合部分图形的各边长度,从而得解;
(3)根据(1)、(2)所求结果,表示出四边形PDEF的面积为PDDE=12t2、梯形PMBD的面积为![]() (PM+BD)·PD=
(PM+BD)·PD=![]() ×[
×[![]() (8-5t)+10-4t]×3t,,根据题意列出方程,解之可得.
(8-5t)+10-4t]×3t,,根据题意列出方程,解之可得.
(1)如图1,当点F落在BC上时,

∵AC=8 cm,BC=6 cm,∠C=90°,
∴AB=10cm,
由题意知,AP=5t,
∵四边形PDEF为矩形,
∴∠PDA=∠C=90°,PF∥AB,PF=DE,
∵∠A=∠A,
∴△APD∽△ABC,
∴![]() =
=![]() =
=![]() ,即
,即![]() =
=![]() =
=![]() ,则AD=4t,PD=3t,
,则AD=4t,PD=3t,
∴PC=AC-AP=8-5t,PF=DE=AD=4t,
∵PF∥AB,
∴△CPF∽△CAB,
∴![]() ,即
,即![]() ,
,
解得t=![]() ;
;
(2)①如图2,当0<t≤![]() 时,
时,
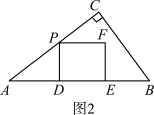
由(1)知,PD=EF=3t,PF=DE=4t,则y=2(3t+4t)=14t;
②如图3,当![]() <t≤
<t≤![]() 时,
时,
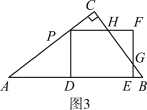
∵AP=5t,AD=DE=4t,
∴PC=8-5t,BE=10-8t,
由△CPH∽△CAB知,![]() ,即
,即![]() ,
,
解得PH=![]() (8-5t),CH=
(8-5t),CH=![]() (8-5t),
(8-5t),
由△BEG∽△BCA知,![]() ,即
,即![]() ,
,
解得EG=![]() (10-8t),BG=
(10-8t),BG=![]() (10-8t),
(10-8t),
则HG=BC-CH-BG=6-![]() (8-5t)-
(8-5t)-![]() (10-8t)=
(10-8t)=![]() t-
t-![]() ,
,
∴y=3t+4t+![]() (8-5t)+
(8-5t)+![]() t-
t-![]() +
+![]() (10-8t)=
(10-8t)=![]() t+
t+![]() ,
,
③如图4,当![]() ≤t≤
≤t≤![]() 时,
时,
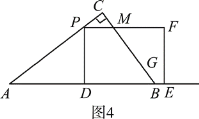
∵AP=5t,AD=DE=4t,PD=3t,
∴PC=8-5t,BD=AB-AD=10-4t,
由②知,PM=![]() (8-5t),CM=
(8-5t),CM=![]() (8-5t),则BM=BC-CM=6-
(8-5t),则BM=BC-CM=6-![]() (8-5t)=
(8-5t)=![]() t,
t,
∴y=3t+10-4t+![]() (8-5t)+
(8-5t)+![]() t=-
t=-![]() t+20;
t+20;
(3)如图4,
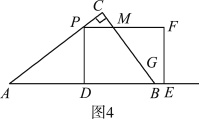
由(1)知,四边形PDEF的面积为PD·DE=3t·4t=12t2,
由(2)得梯形PMBD的面积为![]() (PM+BD)·PD=
(PM+BD)·PD=![]() ×[
×[![]() (8-5t)+10-4t]×3t,
(8-5t)+10-4t]×3t,
∴根据题意得:![]() ×[
×[![]() (8-5t)+10-4t]×3t=
(8-5t)+10-4t]×3t=![]() ×12t2,
×12t2,
解得t=![]() ,
,
故答案为:![]() .
.


 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案科目:初中数学 来源: 题型:
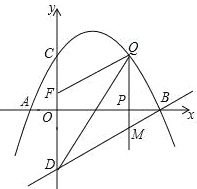
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于![]() 轴对称,点P是
轴对称,点P是![]() 轴上的一个动点,设点P的坐标为(
轴上的一个动点,设点P的坐标为(![]() ,0),过点P做
,0),过点P做![]() 轴的垂线l交抛物线于点Q,交直线BD于点M.
轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB运动过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),当点P在
),当点P在![]() 轴上运动时,试求
轴上运动时,试求![]() 为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为4,点
的边长为4,点![]() 在对角线
在对角线![]() 上(可与点
上(可与点![]() 重合),
重合),![]() ,点
,点![]() 在正方形的边上.下面四个结论中,
在正方形的边上.下面四个结论中,
①存在无数个四边形![]() 是平行四边形;
是平行四边形;
②存在无数个四边形![]() 是菱形;
是菱形;
③存在无数个四边形![]() 是矩形;
是矩形;
④至少存在一个四边形![]() 是正方形.
是正方形.
所有正确结论的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
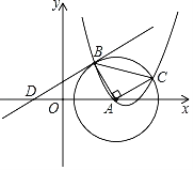
【题目】如图,已知的圆心为点![]() ,抛物线y=ax2﹣
,抛物线y=ax2﹣![]() x+c过点A,与
x+c过点A,与![]() 交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
(1)求B、C点坐标和抛物线的解析式;
(2)直线y=kx+1经过点B,与x轴交于点D.点E(与点D不重合)在该直线上,且AD=AE,请判断点E是否在此抛物线上,并说明理由;
(3)如果直线y=k1x﹣1与⊙A相切,请直接写出满足此条件的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
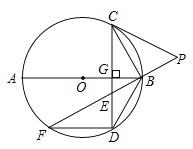
【题目】如图,![]() 为
为![]() 的直径,
的直径,![]() 于点
于点![]() ,
,![]() 是
是![]() 上一点,且
上一点,且![]() ,延长
,延长![]() 至点
至点![]() ,连接
,连接![]() ,使
,使![]() ,延长
,延长![]() 与
与![]() 交于点
交于点![]() ,连结
,连结![]() ,
,![]() .
.
(1)连结![]() ,求证:
,求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线;
的切线;
(3)若![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,图①是一个三角形,分别连接三边中点得图②,再分别连接图②中的小三角形三边中点,得图③……按此方法继续下去.

在第![]() 个图形中有______个三角形(用含
个图形中有______个三角形(用含![]() 的式子表示)
的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】西安市的大雁塔又名“慈恩寺塔”,是国家级文物保护单位,玄奘为保存由天竺经丝绸之路带回长安的经卷主持修建了大雁塔,最初五层,后加盖至九层,是西安市的标志性建筑之一,某校社会实践小组为了测量大雁塔的高度,在地面上C处垂直于地面竖立了高度为2米的标杆CD,这时地面上的点E,标杆的顶端点D,大雁塔的塔尖点B正好在同一直线上,测得EC=4米,将标杆CD向后平移到点G处,这时地面上的点F,标杆的顶端点H,大雁塔的塔尖点B正好在同一直线上(点F,点G,点E,点C与塔底处的点A在同一直线上),这时测得FG=6米,GC=53米,请你根据以上数据,计算大雁塔的高度AB.

查看答案和解析>>
科目:初中数学 来源: 题型:
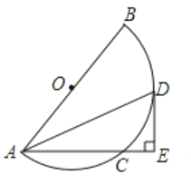
【题目】如图,![]() 是半圆的直径,
是半圆的直径,![]() 为半圆
为半圆![]() 的圆心,
的圆心,![]() 是弦,取
是弦,取![]() 的中点
的中点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是半圆
是半圆![]() 的切线;
的切线;
(2)当![]() ,
,![]() 时,求
时,求![]() 的长;
的长;
(3)当![]() 时,直接写出
时,直接写出![]() 面积最大时,点
面积最大时,点![]() 到直径
到直径![]() 的距离.
的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com