
【题目】正方形![]() 的边长为4,点
的边长为4,点![]() 在对角线
在对角线![]() 上(可与点
上(可与点![]() 重合),
重合),![]() ,点
,点![]() 在正方形的边上.下面四个结论中,
在正方形的边上.下面四个结论中,
①存在无数个四边形![]() 是平行四边形;
是平行四边形;
②存在无数个四边形![]() 是菱形;
是菱形;
③存在无数个四边形![]() 是矩形;
是矩形;
④至少存在一个四边形![]() 是正方形.
是正方形.
所有正确结论的序号是_______.
【答案】①②④
【解析】
根据平行四边形的判定和性质,菱形的判定,矩形的判定,正方形的判定定理即可得到结论.
解:①设正方形的对角线相交于点O,若MN的中点恰好是点O,则经过点O任意一直线PQ,分别与正方形的边AD,BC交于点P,G,通过正方形的性质对称性易得OP=OG,则四边形PMQN是平行四边形,由于PQ的任意性,则存在无数个四边形![]() 是平行四边形,故①正确;
是平行四边形,故①正确;
②过MN的中点E作垂线,分别与正方形的相邻两边交于P,Q,根据正方形的对称性可得,PE=GE,则四边形![]() 是菱形,由于MN的任意性,则存在四边形
是菱形,由于MN的任意性,则存在四边形![]() 是菱形;③由①存在由无数个平行四边边形,要是的四边形为正方形则PQ=MN=2=CD,故此时PQ经过正方形对角线的交点,且与正方形的边BC垂直,是唯一的,故不存在无数个四边形
是菱形;③由①存在由无数个平行四边边形,要是的四边形为正方形则PQ=MN=2=CD,故此时PQ经过正方形对角线的交点,且与正方形的边BC垂直,是唯一的,故不存在无数个四边形![]() 是矩形;④由②知存在菱形,故只需满足∠PMQ=90°时,则四边形PMQN时正方形,此时M与点A重合即可,故存在至少存在一个四边形
是矩形;④由②知存在菱形,故只需满足∠PMQ=90°时,则四边形PMQN时正方形,此时M与点A重合即可,故存在至少存在一个四边形![]() 是正方形;
是正方形;
故正确的结论序号是①②④.


 轻松暑假总复习系列答案
轻松暑假总复习系列答案科目:初中数学 来源: 题型:
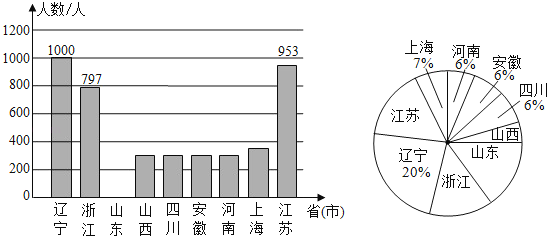
【题目】2020年春节前夕“新型冠状病毒”爆发,疫情就是命令,防控就是使命.全国各地驰援武汉的医护工作者,践行医者仁心的使命与担当,舍小家,为大家,用自己的专业知识与血肉之躯构筑起全社会抗击疫情的钢铁长城.下面是2月9日当天全国部分省市驰援武汉医护工作者的人数统计图(不完整).
请解答下列问题:
(1)①上述省市2月9日当天驰援武汉的医护工作者的总人数为 人;
②请将条形统计图补充完整;
(2)请求出扇形统计图中“山东”所对应扇形的圆心角的度数;
(3)本次山东驰援武汉的医护工作者中,有5人报名去重症区,王医生和李医生就在其中,若从报名的5人中随机安排2人,求同时安排王医生和李医生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了如下的统计图1和图2,请根据图中相关信息,解决下列问题:
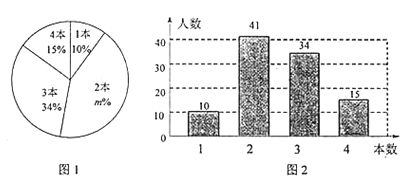
(Ⅰ)图1中![]() 的值为____________,共有____________名同学参与问卷调查;
的值为____________,共有____________名同学参与问卷调查;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)全校共有学生1500人,根据样本数据,估计该校学生一个月阅读2本课外书的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数![]() 的图象和性质进行了探究,探究过程如下,请补充完整.
的图象和性质进行了探究,探究过程如下,请补充完整.
(1)自变量![]() 的取值范围是全体实数,
的取值范围是全体实数,![]() 与
与![]() 的几组对应值列表如下:
的几组对应值列表如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中,![]() .
.
(2)根据上表数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该函数图象的另一部分.
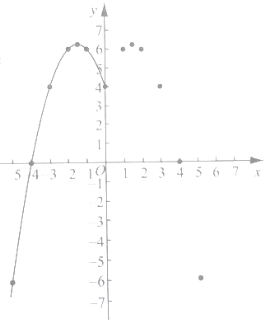
(3)观察函数图象,写出两条函数的性质.
(4)直线![]() 经过
经过![]() ,若关于
,若关于![]() 的方程
的方程![]() 有
有![]() 个不相等的实数根,则
个不相等的实数根,则![]() 的取值范围为 .
的取值范围为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校从甲、乙两名班主任中选拔一名参加教育局组织的班主任技能比赛,选拔内容分案例分析、班会设计、情景问答三个项目,选拔比赛结束后,统计的这两位班主任成绩并制成了如图所示的条形统计图:
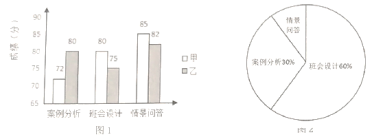
(1)乙班主任三个项目的成绩中位数是______________________;
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“80”的概率;
(3)若按照图2所示的权重比进行计算,选拔分数最高的一名班主任参加比赛,应确定哪名班主任获得参赛资格,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与y轴交于点
与y轴交于点![]() .
.
(1)求c的值;
(2)当![]() 时,求抛物线顶点的坐标;
时,求抛物线顶点的坐标;
(3)已知点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有两个公共点,结合函数图象,求a的取值范围.
有两个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明为探究函数![]() 的图象和性质,需要画出函数图象,列表如下:
的图象和性质,需要画出函数图象,列表如下:
| …… |
|
|
|
|
|
|
|
|
|
| …… |
| …… |
|
|
|
|
|
|
|
|
|
| …… |
根据上表数据,在平面直角坐标系中描点,画出函数图象,如图如示,小明画出了图象的一部分.
(1)请你帮小明画出完整的![]() 的图象;
的图象;
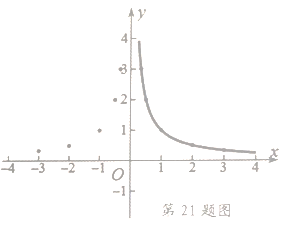
(2)观察函数图象,请写出这个函数的两条性质:
性质一: ;
性质二: .
(3)利用上述图象,探究函数![]() 图象与直线
图象与直线![]() 的关系;
的关系;
①当![]() 时, 直线
时, 直线![]() 与函数
与函数![]() 在第一象限的图象有一个交点
在第一象限的图象有一个交点![]() ,则
,则![]() 的坐标是 ;
的坐标是 ;
②当![]() 为何值时,讨论函数
为何值时,讨论函数![]() 的图象与直线
的图象与直线![]() 的交点个数.
的交点个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠C=90°,AC=8 cm,BC=6 cm.动点P在线段AC上以5 cm/s的速度从点A运动到点C.过点P作PD⊥AB于点D,以PD为一边向右作矩形PDEF,并且使DE=AD.设点P的运动时间为t s,矩形PDEF和△ABC重叠部分图形周长为y cm.
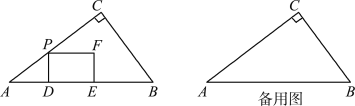
(1)当点F落在边BC上时,求t的值;
(2)求y与t之间的函数关系式;
(3)当矩形PDEF的面积被线段BC平分时,t=______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴的交点为
轴的交点为![]() ,与
,与![]() 轴的交点分别为
轴的交点分别为![]() ,
,![]() ,且
,且![]() ,直线
,直线![]() 轴,在
轴,在![]() 轴上有一动点
轴上有一动点![]() 过点
过点![]() 作平行于
作平行于![]() 轴的直线
轴的直线![]() 与抛物线、直线
与抛物线、直线![]() 的交点分别为
的交点分别为![]() 、
、![]() .
.
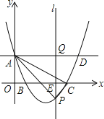
![]() 求抛物线的解析式;
求抛物线的解析式;
![]() 当
当![]() 时,求
时,求![]() 面积的最大值;
面积的最大值;
![]() 当
当![]() 时,是否存在点
时,是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 为顶点的三角形与
为顶点的三角形与![]() 相似?若存在,求出此时
相似?若存在,求出此时![]() 的值;若不存在,请说明理由.
的值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com