
【题目】某学校从甲、乙两名班主任中选拔一名参加教育局组织的班主任技能比赛,选拔内容分案例分析、班会设计、情景问答三个项目,选拔比赛结束后,统计的这两位班主任成绩并制成了如图所示的条形统计图:
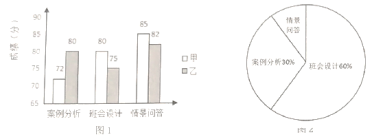
(1)乙班主任三个项目的成绩中位数是______________________;
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“80”的概率;
(3)若按照图2所示的权重比进行计算,选拔分数最高的一名班主任参加比赛,应确定哪名班主任获得参赛资格,说明理由.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案科目:初中数学 来源: 题型:
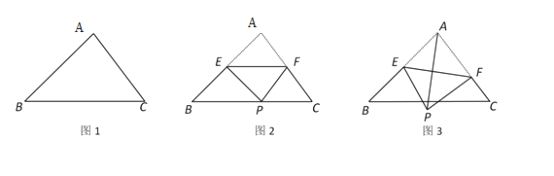
【题目】如图,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() .过点
.过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求该抛物线的解析式及对称轴;
(Ⅱ)点![]() 在
在![]() 轴上,当
轴上,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(Ⅲ)抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
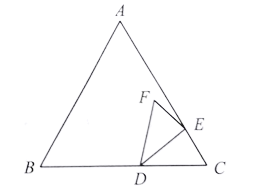
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AB边上的动点,过点D作DE⊥AB交边AC于点E,过点E作EF⊥DE交BC于点F,连接DF.
(1)当AD=4时,求EF的长度;
(2)求△DEF的面积的最大值;
(3)设O为DF的中点,随着点D的运动,则点O的运动路径的长度为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 中,
中,![]() 点
点![]() 在边
在边![]() 上,
上,![]() .点
.点![]() 为边
为边![]() 上一动点(不与点
上一动点(不与点![]() 重合),连接
重合),连接![]() 关于
关于![]() 的轴对称图形为
的轴对称图形为![]() .
.
(1)当点![]() 在
在![]() 上时,求证:
上时,求证:![]() ;
;
(2)当![]() 三点共线时,求
三点共线时,求![]() 的长;
的长;
(3)连接![]() 设
设![]() 的面积为
的面积为![]() 的面积为
的面积为![]() 记
记![]()
![]() 是否存在最大值?若存在,请直接写出
是否存在最大值?若存在,请直接写出![]() 的最大值;若不存在,请说明理由.
的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】正方形![]() 的边长为4,点
的边长为4,点![]() 在对角线
在对角线![]() 上(可与点
上(可与点![]() 重合),
重合),![]() ,点
,点![]() 在正方形的边上.下面四个结论中,
在正方形的边上.下面四个结论中,
①存在无数个四边形![]() 是平行四边形;
是平行四边形;
②存在无数个四边形![]() 是菱形;
是菱形;
③存在无数个四边形![]() 是矩形;
是矩形;
④至少存在一个四边形![]() 是正方形.
是正方形.
所有正确结论的序号是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
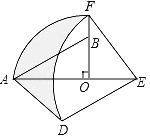
【题目】如图,在Rt△AOB中,∠AOB=90°,OA=3,OB=2,将Rt△AOB绕点O顺时针旋转90°后得Rt△FOE,将线段EF绕点E逆时针旋转90°后得线段ED,分别以O,E为圆心,OA、ED长为半径画弧AF和弧DF,连接AD,则图中阴影部分面积是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
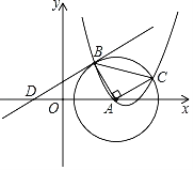
【题目】如图,已知的圆心为点![]() ,抛物线y=ax2﹣
,抛物线y=ax2﹣![]() x+c过点A,与
x+c过点A,与![]() 交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
(1)求B、C点坐标和抛物线的解析式;
(2)直线y=kx+1经过点B,与x轴交于点D.点E(与点D不重合)在该直线上,且AD=AE,请判断点E是否在此抛物线上,并说明理由;
(3)如果直线y=k1x﹣1与⊙A相切,请直接写出满足此条件的直线解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为提高饮水质量,越来越多的居民开始选购家用净水器.一商家抓住商机,从厂家购进了A、B两种型号家用净水器共160台,A型号家用净水器进价是150元/台,B型号家用净水器进价是350元/台,购进两种型号的家用净水器共用去36000元.
(1)求A、B两种型号家用净水器各购进了多少台;
(2)为使每台B型号家用净水器的毛利润是A型号的2倍,且保证售完这160台家用净水器的毛利润不低于11000元,求每台A型号家用净水器的售价至少是多少元?(注:毛利润=售价﹣进价)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com