
【题目】在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() .过点
.过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求该抛物线的解析式及对称轴;
(Ⅱ)点![]() 在
在![]() 轴上,当
轴上,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(Ⅲ)抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(Ⅰ)抛物线的解析式为![]() ;抛物线的对称轴为直线
;抛物线的对称轴为直线![]() ;(Ⅱ)
;(Ⅱ)![]() 点坐标为
点坐标为![]() ;(Ⅲ)存在,
;(Ⅲ)存在,![]() 点坐标为
点坐标为![]() 或
或![]() ,理由见解析
,理由见解析
【解析】
(Ⅰ)将![]() 点代入二次函数的解析式,即可求出a,再根据对称轴的公式即可求解.
点代入二次函数的解析式,即可求出a,再根据对称轴的公式即可求解.
(Ⅱ)先求出B点胡坐标,要求![]() 胡最小值,只需找到B关于轴的对称点
胡最小值,只需找到B关于轴的对称点![]() ,则直线A
,则直线A![]() 与y轴的交点就是点P,根据待定系数法求出AB1的解析式,令y=0,即可求出P点的坐标.
与y轴的交点就是点P,根据待定系数法求出AB1的解析式,令y=0,即可求出P点的坐标.
(Ⅲ)设点Q的坐标,并求出△AOQ面积,从而得到△AOQ面积,根据Q点胡不同位置进行分类,用m及割补法求出面积方程,即可求解.
(Ⅰ)∵![]() 经过点
经过点![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴抛物线的解析式为![]() ,
,
∵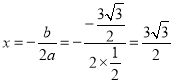 ,
,
∴抛物线的对称轴为直线![]() .
.
(Ⅱ)∵点![]() ,对称轴为
,对称轴为![]() ,
,
∴点![]() 关于对称轴的对称点
关于对称轴的对称点![]() 点坐标为
点坐标为![]() .
.
作点![]() 关于轴的对称点
关于轴的对称点![]() ,得
,得![]() ,
,
设直线AB1的解析式为![]() ,
,
把点![]() ,点
,点![]() 代入得
代入得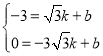 ,
,
解得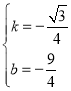 ,∴
,∴![]() .
.
∴直线![]() 与
与![]() 轴的交点即为
轴的交点即为![]() 点.
点.
令![]() 得
得![]() ,
,
∵![]() 点坐标为
点坐标为![]() .
.
(Ⅲ)∵![]() ,
,![]() 轴,∴
轴,∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
设![]() 点坐标为
点坐标为![]() ,
,
如图情况一,作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,
,
∵![]() ,
,
∴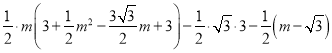
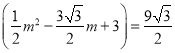 ,
,
化简整理得![]() ,
,
解得![]() ,
,![]() .
.
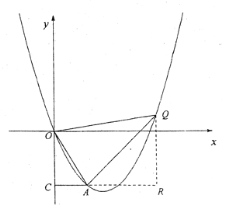
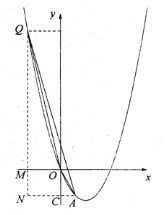
如图情况二,作![]() ,交
,交![]() 延长线于点
延长线于点![]() ,交
,交![]() 轴于点
轴于点![]() ,
,
∵![]() ,
,
∴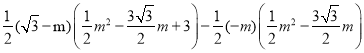
![]() ,
,
化简整理得![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() 点坐标为
点坐标为![]() 或
或![]() ,
,
∴抛物线上存在点![]() ,使得
,使得![]() .
.


 通城学典默写能手系列答案
通城学典默写能手系列答案科目:初中数学 来源: 题型:
【题目】新冠肺炎疫情防控期间,学校为做好预防性消毒工作,开学初购进![]() 、
、![]() 两种消毒液,其中
两种消毒液,其中![]() 消毒液的单价比
消毒液的单价比![]() 消毒液的单价多
消毒液的单价多![]() 元,用
元,用![]() 元购买
元购买![]() 消毒液的数量是用
消毒液的数量是用![]() 元购买
元购买![]() 消毒液数量的
消毒液数量的![]() 倍.
倍.
(1)求两种消毒液的单价;
(2)学校准备用不多于![]() 元的资金购买
元的资金购买![]() 、
、![]() 两种消毒液共
两种消毒液共![]() 桶,问最多购买
桶,问最多购买![]() 消毒液多少桶?
消毒液多少桶?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了让学生更好地树立“安全第一,预防为主”的思想,某学校开展了“2020校园预防新冠肺炎知识竞赛”活动,若让知识竞赛的成绩分为:A(优秀)、B(良好)、C(合格)、D(不合格)四个等级,张老师从中抽取若干名学生的成绩进行统计,并将统计结果绘制成如图所示的扇形和条形统计图,请结合图中所给信息回答下列问题:

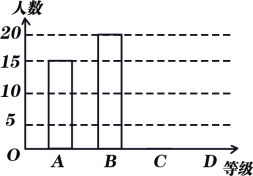
(1)本次被调查的对象共有 人;被调查者“不合格”有 人;
(2)将条形统计图补充完整;
(3)假设这所学校有2000名学生,请据此估计“良好”的学生有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】央视“经典咏流传”开播以来受到社会广泛关注,我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:
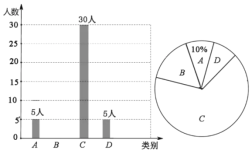
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”
(1)被调查的总人数是________人,扇形统计图中C部分所对应的扇形圆心角的度数为______;
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中D类有______人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
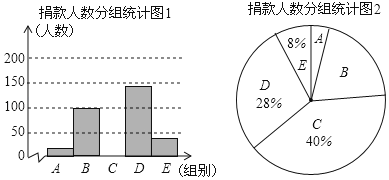
【题目】某校学生会干部对全校师生倡导的“武汉加油”的自愿捐款活动进行抽样调查,得到一组学生捐款情况的数据,对学校部分捐款人数进行调查和分组统计后,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1∶5.
组别 | 捐款额x(元) | 人数 |
A | 1≤x<10 | a |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | 40≤x<50 |
请结合以上信息解答下列问题.
(1)a= ,本次调查样本的容量是 ;
(2)先求出C组的人数,再补全“捐款人数分组统计图1”;
(3)根据统计情况,估计该校参加捐款的5000名学生有多少人捐款在20至50元之间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班研究性学习小组为研究全校同学课外阅读情况,在全校随机邀请了部分同学参与问卷调查,统计同学们一个月阅读课外书的数量,并绘制了如下的统计图1和图2,请根据图中相关信息,解决下列问题:
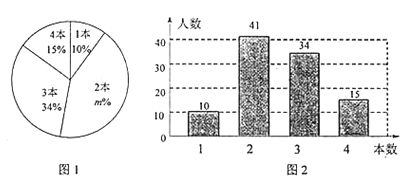
(Ⅰ)图1中![]() 的值为____________,共有____________名同学参与问卷调查;
的值为____________,共有____________名同学参与问卷调查;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ)全校共有学生1500人,根据样本数据,估计该校学生一个月阅读2本课外书的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020蓉漂云招聘活动在4月25日正式启动,共发布了岗位13198个.某网络公司招聘一名高级网络工程师,应聘者小魏参加笔试和面试,成绩(100分制)如表所示:
笔试 | 面试 | |||||||
成绩 | 98 | 评委1 | 评委2 | 评委3 | 评委4 | 评委5 | 评委6 | 评委 7 |
94 | 95 | 92 | 99 | 98 | 97 | 96 | ||
其中规定:面试得分中去掉一个最高分和一个最低分,余下的面试得分的平均值作为应聘者的面试成绩.
(1)请计算小魏的面试成绩;
(2)如果面试成绩与笔试成绩按6:4的比例确定,请计算出小魏的最终成绩.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校从甲、乙两名班主任中选拔一名参加教育局组织的班主任技能比赛,选拔内容分案例分析、班会设计、情景问答三个项目,选拔比赛结束后,统计的这两位班主任成绩并制成了如图所示的条形统计图:
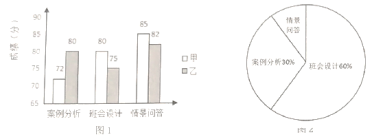
(1)乙班主任三个项目的成绩中位数是______________________;
(2)用6张相同的卡片分别写上甲、乙两名班主任的六项成绩,洗匀后,从中任意抽取一张,求抽到的卡片写有“80”的概率;
(3)若按照图2所示的权重比进行计算,选拔分数最高的一名班主任参加比赛,应确定哪名班主任获得参赛资格,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
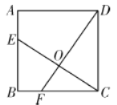
【题目】如图,已知正方形![]() 的边长为
的边长为![]() ,点
,点![]() ,
,![]() 分别在边
分别在边![]() ,
,![]() 上,且
上,且![]() ,
,![]() ,
,![]() 相交于点
相交于点![]() ,下列结论:①
,下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() 的面积等于四边形
的面积等于四边形![]() 的面积,其中正确的有( )
的面积,其中正确的有( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com