
【题目】央视“经典咏流传”开播以来受到社会广泛关注,我市某校就“中华文化我传承——地方戏曲进校园”的喜爱情况进行了随机调查,对收集的信息进行统计,绘制了下面两副尚不完整的统计图,请你根据统计图所提供的信息解答下列问题:
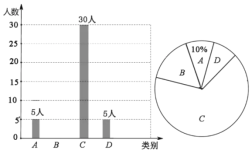
图中A表示“很喜欢”,B表示“喜欢”,C表示“一般”,D表示“不喜欢”
(1)被调查的总人数是________人,扇形统计图中C部分所对应的扇形圆心角的度数为______;
(2)补全条形统计图;
(3)若该校共有学生1800人,请根据上述调查结果,估计该校学生中D类有______人;
(4)在抽取的A类5人中,刚好有3个女生2个男生,从中随机抽取两个同学担任两角色,用树形图或列表法求出被抽到的两个学生性别相同的概率.
【答案】(1)50;216°;(2)见解析;(3)180;(4)![]()
【解析】
(1)由A的人数除以所占百分比得出被调查的总人数,由360乘以C所占比例即可求得C部分所对应的扇形圆心角的度数;
(2)求出B部分的人数,补全条形统计图;
(3)由该校总人数乘以D类所占比例即可得出答案;
(4)由列表法和概率公式即可解答.
(1)5÷10%=50(人),
360×![]() =216,
=216,
故答案为:50;216°;
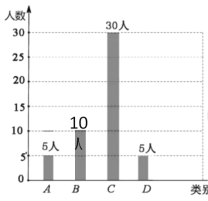
(2)如图所示,总人数为50人,所以B的人数=50-5-30-5=10(人),补全条形统计图如图:
(3)1800 ×![]() =180 (人),
=180 (人),
故答案为:180;
(4)设3个女生分别为女1,女2,女3,2个男生分别为男1,男2,所有可能出现的结果如下表:
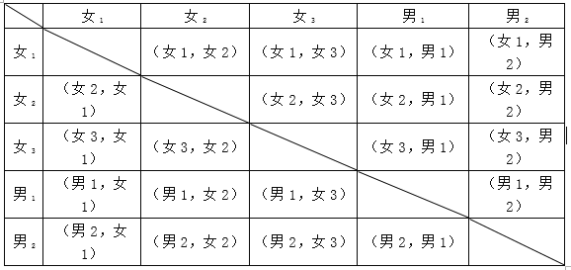
从中随机抽取两个同学担任两角色,所有可能的结果有20种,每种结果的可能性都相同,其中,抽到性别相同的结果有8种,
所以P(被抽到的两个学生性别相同)=![]() .
.


科目:初中数学 来源: 题型:
【题目】观察以下等式:
第1个等式:23-22=13+2×1+1;
第2个等式:33-32=23+3×2+22;
第3个等式:43-42=33+4×3+32;
……
按照以上规律,解决下列问题:
(1)写出第4个等式:__________________;
(2)写出你猜想的第n个等式(用含n的等式表示),并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=![]() ,∠B=45°,∠C=60°.
,∠B=45°,∠C=60°.
(1)求BC边上的高线长.
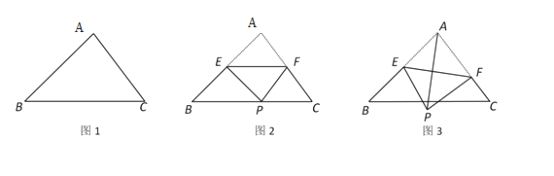
(2)点E为线段AB的中点,点F在边AC上,连结EF,沿EF将△AEF折叠得到△PEF.
①如图2,当点P落在BC上时,求∠AEP的度数.
②如图3,连结AP,当PF⊥AC时,求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
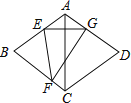
【题目】如图,已知四边形ABCD是边长为6的菱形,且∠BAD=120°,点E,F分别在AB、BC边上,将菱形沿EF折叠,点B正好落在AD边的点G处,若EG⊥AC,则FG的长为( )
A.3![]() B.6C.3
B.6C.3![]() D.3
D.3![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
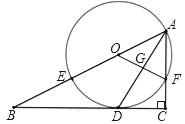
【题目】如图,在Rt△ABC中,∠C=90°,AD平分∠BAC交BC于点D,O为AB上一点,经过点A,D的⊙O分别交AB,AC于点E,F,连接OF交AD于点G.
(1)求证:BC是⊙O的切线;
(2)设AB=x,AF=y,试用含x,y的代数式表示线段AD的长;
(3)若BE=8,sinB=![]() ,求DG的长,
,求DG的长,
查看答案和解析>>
科目:初中数学 来源: 题型:
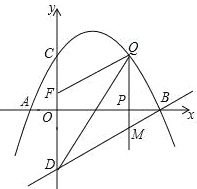
【题目】如图,已知抛物线经过点A(﹣1,0),B(4,0),C(0,2)三点,点D与点C关于![]() 轴对称,点P是
轴对称,点P是![]() 轴上的一个动点,设点P的坐标为(
轴上的一个动点,设点P的坐标为(![]() ,0),过点P做
,0),过点P做![]() 轴的垂线l交抛物线于点Q,交直线BD于点M.
轴的垂线l交抛物线于点Q,交直线BD于点M.
(1)求该抛物线所表示的二次函数的表达式;
(2)点P在线段AB运动过程中,是否存在点Q,使得△BOD∽△QBM?若存在,求出点Q的坐标;若不存在,请说明理由.
(3)已知点F(0,![]() ),当点P在
),当点P在![]() 轴上运动时,试求
轴上运动时,试求![]() 为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
为何值时,以D,M,Q,F为顶点的四边形是平行四边形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,![]() 为原点,抛物线
为原点,抛物线![]() 经过点
经过点![]() ,对称轴为直线
,对称轴为直线![]() ,点
,点![]() 关于直线
关于直线![]() 的对称点为点
的对称点为点![]() .过点
.过点![]() 作直线
作直线![]() 轴,交
轴,交![]() 轴于点
轴于点![]() .
.
(Ⅰ)求该抛物线的解析式及对称轴;
(Ⅱ)点![]() 在
在![]() 轴上,当
轴上,当![]() 的值最小时,求点
的值最小时,求点![]() 的坐标;
的坐标;
(Ⅲ)抛物线上是否存在点![]() ,使得
,使得![]() ,若存在,求出点
,若存在,求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AB边上的动点,过点D作DE⊥AB交边AC于点E,过点E作EF⊥DE交BC于点F,连接DF.
(1)当AD=4时,求EF的长度;
(2)求△DEF的面积的最大值;
(3)设O为DF的中点,随着点D的运动,则点O的运动路径的长度为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
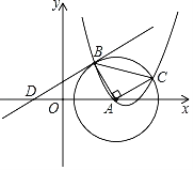
【题目】如图,已知的圆心为点![]() ,抛物线y=ax2﹣
,抛物线y=ax2﹣![]() x+c过点A,与
x+c过点A,与![]() 交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
交于B、C两点,连接AB、AC,且AB⊥AC,B、C两点的纵坐标分别是2、1.
(1)求B、C点坐标和抛物线的解析式;
(2)直线y=kx+1经过点B,与x轴交于点D.点E(与点D不重合)在该直线上,且AD=AE,请判断点E是否在此抛物线上,并说明理由;
(3)如果直线y=k1x﹣1与⊙A相切,请直接写出满足此条件的直线解析式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com