
����Ŀ��ij�ࡰ��ѧ��ȤС�顱�Ժ���![]() ��ͼ������ʽ�����̽����̽���������£��벹��������
��ͼ������ʽ�����̽����̽���������£��벹��������
��1���Ա���![]() ��ȡֵ��Χ��ȫ��ʵ����
��ȡֵ��Χ��ȫ��ʵ����![]() ��
��![]() �ļ����Ӧֵ�б����£�
�ļ����Ӧֵ�б����£�
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
����![]() ����������
����������
��2�������ϱ����ݣ�����ͼ��ʾ��ƽ��ֱ������ϵ����㣬�������˺���ͼ���һ���֣��뻭���ú���ͼ�����һ���֣�
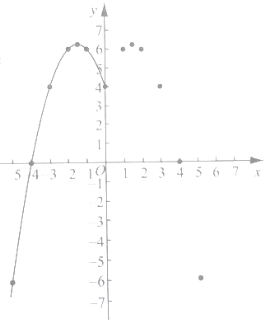
��3���۲캯��ͼ��д���������������ʣ�
��4��ֱ��![]() ����
����![]() ��������
��������![]() �ķ���
�ķ���![]() ��
��![]() ������ȵ�ʵ��������
������ȵ�ʵ��������![]() ��ȡֵ��ΧΪ����������
��ȡֵ��ΧΪ����������
���𰸡���1��-6����2���𰸼���������3���ٸú�����ͼ�����![]() ��Գƣ��ڸú�����ͼ������ߵ㣻��4��
��Գƣ��ڸú�����ͼ������ߵ㣻��4��![]() ��
��
��������
��1�����ݶԳƿɵ�m=-6��
��2����ƽ�����������Ӹ��㼴�ɻ���ͼ�Σ�
��3������۲�ͼ���ܽ��2�����ʼ��ɣ�
��4������������ͼ�ɵõ����ۣ�
��1���ɱ����֪��ͼ��ĶԳ�����y�ᣬ
��m=-6��
�ʴ�Ϊ��-6��
![]() ��ͼ��ʾ
��ͼ��ʾ

![]() �ú�����ͼ�����
�ú�����ͼ�����![]() ��Գ�
��Գ�
![]() �ú�����ͼ������ߵ㣻
�ú�����ͼ������ߵ㣻
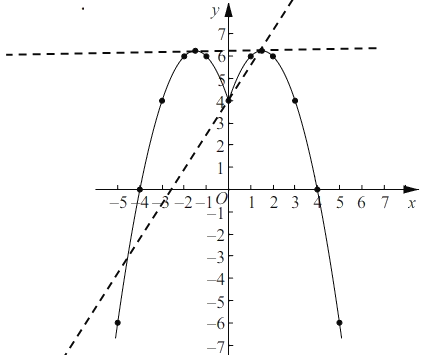
��4����ͼ���֪������![]() �ķ���
�ķ���![]() ��
��![]() ������ȵ�ʵ����ʱ��
������ȵ�ʵ����ʱ��
��y=kx+bʱ����ͼ����4�����㣬
���ԣ���ͼ����Եó�����![]() ʱ��ֱ����ͼ����4����ͬ�Ľ��㣮
ʱ��ֱ����ͼ����4����ͬ�Ľ��㣮
�ʴ�Ϊ��![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
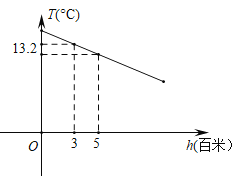
����Ŀ��ij����ɽ��ĸ߶�ÿ����1���ף����´�Լ����0.6��.����T(��)�߶�h(����)�ĺ�����ϵ��ͼ��ʾ.�����ͼ�����������⣺
��1����߶�Ϊ5����ʱ�����£�
��2����T����h�ĺ�������ʽ��
��3�����ɽ��������Ϊ6�������ɽ��ĸ߶ȣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
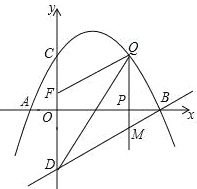
����Ŀ����ͼ����֪�����߾�����A����1��0����B��4��0����C��0��2�����㣬��D���C����![]() ��Գƣ���P��
��Գƣ���P��![]() ���ϵ�һ�����㣬���P������Ϊ��
���ϵ�һ�����㣬���P������Ϊ��![]() ��0��������P��
��0��������P��![]() ��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��Ĵ���l���������ڵ�Q����ֱ��BD�ڵ�M��
��1���������������ʾ�Ķ��κ����ı���ʽ��
��2����P���߶�AB�˶������У��Ƿ���ڵ�Q��ʹ����BOD�ס�QBM�������ڣ������Q�����ꣻ�������ڣ���˵�����ɣ�
��3����֪��F��0��![]() ��������P��
��������P��![]() �����˶�ʱ������
�����˶�ʱ������![]() Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
Ϊ��ֵʱ����D��M��Q��FΪ������ı�����ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������A0B0C0A1�ı߳�Ϊ1��������A1B1C1A2�ı߳�Ϊ2��������A2B2C2A3�ı߳�Ϊ4��������A3B3C3A4�ı߳�Ϊ8�������˹��ɼ�����������AnBnnAn+1���ҵ�A0��A1��A2��A3������An+1��ͬһ��ֱ���ϣ�����A0C1��A1B1�ڵ�D1������A1C2��A2B2�ڵ�D2������A2C3��A3B3�ڵ�D3�������ı���A0B0C0D1�����ΪS1���ı���A1B1C1D2�����ΪS2���ı���A2B2C2D3�����ΪS3�����ı���An��1Bn��1Cn��1Dn�����ΪSn����S2019��_____��
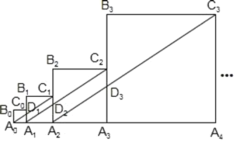
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����Rt��ABC�У���C��90����AC��8��BC��6��DΪAB���ϵĶ��㣬����D��DE��AB����AC�ڵ�E������E��EF��DE��BC�ڵ�F������DF��
��1����AD��4ʱ����EF�ij��ȣ�
��2������DEF����������ֵ��
��3����OΪDF���е㣬���ŵ�D���˶������O���˶�·���ij���Ϊ______��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() ��һ����Ƕ���
��һ����Ƕ���![]() ��
��![]() �ϵ�һ�����㣬
�ϵ�һ�����㣬![]() ����
����![]() ���
��б��![]() �ֱ�
�ֱ�![]() �ڵ�
�ڵ�![]() ���ֱ����
���ֱ����![]() ��
��![]() �����߽��ڵ�
�����߽��ڵ�![]() ���ҵ�
���ҵ�![]() ǡ������
ǡ������![]() �ϵĵ㣬����
�ϵĵ㣬����![]() ����
����![]() �İ뾶Ϊ4����
�İ뾶Ϊ4����![]() �����ֵΪ���� ��
�����ֵΪ���� ��
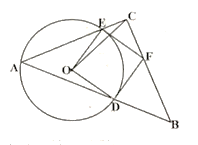
A.![]() B.
B.![]() C.6D.8
C.6D.8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������![]() �ı߳�Ϊ4����
�ı߳�Ϊ4����![]() �ڶԽ���
�ڶԽ���![]() �ϣ������
�ϣ������![]() �غϣ���
�غϣ���![]() ����
����![]() �������εı��ϣ������ĸ������У�
�������εı��ϣ������ĸ������У�
�ٴ����������ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
�ڴ����������ı���![]() �����Σ�
������
�۴����������ı���![]() �Ǿ��Σ�
�Ǿ��Σ�
�����ٴ���һ���ı���![]() �������Σ�
��������
������ȷ���۵������_______��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����߶�ACΪ�Խ��ߵ��ı���ABCD(�����ĸ�����A��B��C��D��˳ʱ�뷽������)����֪AB��BC��CD����ABC��100������CAD��40�������BCD�Ķ���Ϊ________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������еĴ������������ȶ����������ǹ��Ҽ����ﱣ����λ������Ϊ���������þ�˿��֮·���س����ľ����������˴������������㣬��Ӹ����Ų㣬�������еı�־�Խ���֮һ��ijУ���ʵ��С��Ϊ�˲����������ĸ߶ȣ��ڵ�����C����ֱ�ڵ��������˸߶�Ϊ2�ı��CD����ʱ�����ϵĵ�E����˵Ķ��˵�D���������������B������ͬһֱ���ϣ����EC=4�ף������CD���ƽ�Ƶ���G������ʱ�����ϵĵ�F����˵Ķ��˵�H���������������B������ͬһֱ����(��F����G����E����C�����״��ĵ�A��ͬһֱ����)����ʱ���FG=6�ף�GC=53�ף���������������ݣ�����������ĸ߶�AB��

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com