
【题目】以线段AC为对角线的四边形ABCD(它的四个顶点A,B,C,D按顺时针方向排列),已知AB=BC=CD,∠ABC=100°,∠CAD=40°,则∠BCD的度数为________.
【答案】80°或100°
【解析】∵AB=BC,∠ABC=100°,∴∠1=∠2=∠CAD=40°,∴AD∥BC.点D的位置有两种情况:(1)如图①,过点C分别作CE⊥AB于E,CF⊥AD于F,∵∠1=∠CAD,∴CE=CF,
在Rt△ACE与Rt△ACF中, ![]() ,∴Rt△ACE≌Rt△ACF,∴∠ACE=∠ACF.
,∴Rt△ACE≌Rt△ACF,∴∠ACE=∠ACF.
在Rt△BCE与Rt△DCF中, ![]() ,∴Rt△BCE≌Rt△DCF,∴∠BCE=∠DCF,
,∴Rt△BCE≌Rt△DCF,∴∠BCE=∠DCF,
∴∠ACD=∠2=40°,∴∠BCD=80°;
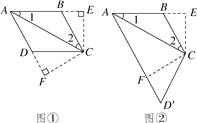
(2)如图②,∵AD′∥BC,AB=CD′,∴四边形ABCD′是等腰梯形,∴∠BCD′=∠ABC=100°,综上所述,∠BCD=80°或100°,
故答案为:80°或100°.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,已知数轴上点A表示的数为8,B是数轴上位于点A左侧一点,且AB=20,
(1)写出数轴上点B表示的数 ;
(2)|5﹣3|表示5与3之差的绝对值,实际上也可理解为5与3两数在数轴上所对的两点之间的距离.如|x﹣3|的几何意义是数轴上表示有理数x的点与表示有理数3的点之间的距离.试探索:
①:若|x﹣8|=2,则x= .
②:|x+12|+|x﹣8|的最小值为 .
(3)动点P从O点出发,以每秒5个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.求当t为多少秒时?A,P两点之间的距离为2;
(4)动点P,Q分别从O,B两点,同时出发,点P以每秒5个单位长度沿数轴向右匀速运动,Q点以P点速度的两倍,沿数轴向右匀速运动,设运动时间为t(t>0)秒.问当t为多少秒时?P,Q之间的距离为4.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我校全体同学参加了二年级刘XX同学的捐款活动,随机抽查了部分同学捐款的情况统计如图所示.
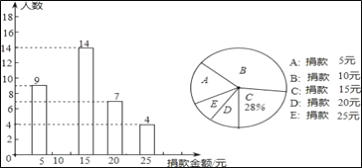
(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 ,平均数是 ;
(3)在我校2200名学生中,捐款15元及以上(含15元)的学生估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知数轴上有三点A、B、C,AB=60,点A对应的数是40.

(1)若![]() ,求点C到原点的距离;
,求点C到原点的距离;
(2)如图2,在(1)的条件下,动点P、Q两点同时从C、A出发向右运动,同时动点R从点A向左运动,已知点P的速度是点R的速度的3倍,点Q的速度是点R的速度2倍少5个单位长度/秒.经过5秒,点P、Q之间的距离与点Q、R之间的距离相等,求动点Q的速度;
(3)如图3,在(1)的条件下,O表示原点,动点P、T分别从C、O两点同时出发向左运动,同时动点R从点A出发向右运动,点P、T、R的速度分别为5个单位长度/秒、1个单位长度/秒、2个单位长度/秒,在运动过程中,如果点M为线段PT的中点,点N为线段OR的中点.请问![]() 的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
的值是否会发生变化?若不变,请求出相应的数值;若变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场销售“喜羊羊”玩具,预测该产品能够畅销,就用32000元购进了一批这种玩具,上市后很快脱销,商场又用68000元购进第二批这种玩具,所购数量是第一批购进数量的2倍,但每个进价多了10元.
(1)该商场两次共购进这种玩具多少个?
(2)如果这两批玩具每套的售价相同,且全部售完后总利润率不低于20%,那么每件售价至少是多少元?(利润率![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
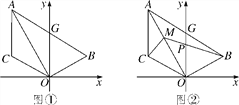
【题目】如图①,已知线段AC∥y轴,点B在第一象限,且AO平分∠BAC,AB交y轴于G,连接OB,OC.
(1)判断△AOG的形状,并予以证明;
(2)若点B,C关于y轴对称,求证:AO⊥BO;
(3)在(2)的条件下,如图②,点M为OA上一点,且∠ACM=45°,BM交y轴于P,若点B的坐标为(3,1),求点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】把正整数1,2,3,4,…,2 009排列成如图所示的一个表.
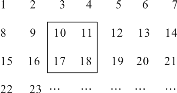
(1)用一正方形在表中随意框住4个数,把其中最小的数记为x,另三个数用含x的式子表示出来,从小到大依次是__ __,__ __,__ __;
(2)在(1)前提下,当被框住的4个数之和等于416时,x的值是多少?
(3)在(1)前提下,被框住的4个数之和能否等于622?如果能,请求出此时x的值;如果不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
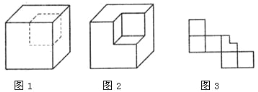
【题目】如图![]() ,大正方体上截去一个小正方体后,可得到图
,大正方体上截去一个小正方体后,可得到图![]() 的几何体.
的几何体.
![]() 设原大正方体的表面积为
设原大正方体的表面积为![]() ,图
,图![]() 中几何体的表面积为
中几何体的表面积为![]() ,那么
,那么![]() 与
与![]() 的大小关系是( )
的大小关系是( )
![]() 、
、![]()
![]() 、
、![]()
![]() 、
、![]()
![]() 、不确定
、不确定
![]() 小明说:“设图
小明说:“设图![]() 中大正方体各棱的长度之和为
中大正方体各棱的长度之和为![]() ,图
,图![]() 中几何体各棱的长度之和为
中几何体各棱的长度之和为![]() ,那么
,那么![]() 比
比![]() 正好多出大正方体
正好多出大正方体![]() 条棱的长度.”若设大正方体的棱长为
条棱的长度.”若设大正方体的棱长为![]() ,小正方体的棱长为
,小正方体的棱长为![]() ,请问
,请问![]() 为何值时,小明的说法才正确?
为何值时,小明的说法才正确?
![]() 如果截去的小正方体的棱长为大正方体棱长的一半,那么图
如果截去的小正方体的棱长为大正方体棱长的一半,那么图![]() 是图
是图![]() 中几何体的表面展开图吗?如有错误,请在图
中几何体的表面展开图吗?如有错误,请在图![]() 中修正.
中修正.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com