
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
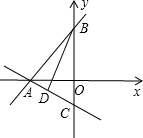 把A(-2,0)代入y=
把A(-2,0)代入y=| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 12+22 |
| 5 |
| 1 |
| 2 |
| 8 | ||
|
8
| ||
| 5 |
8
| ||
| 5 |


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:初中数学 来源: 题型:
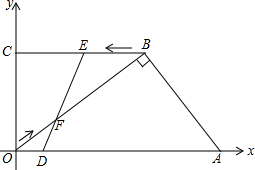 如图,在平面直角坐标系中,A(
如图,在平面直角坐标系中,A(| 25 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
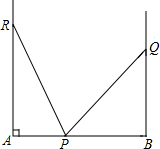 如图,设在一个宽度AB=a的小巷内,一个梯子的长度为b,梯子的脚位于P点,将该梯子的顶端放于一堵墙上Q点时,Q点离地面的高度为c,梯子与地面的夹角为45°,将梯子顶端放于对面一堵墙上R点,离开地面的高度为d,此时梯子与地面的夹角为75°,则d=a,为什么?
如图,设在一个宽度AB=a的小巷内,一个梯子的长度为b,梯子的脚位于P点,将该梯子的顶端放于一堵墙上Q点时,Q点离地面的高度为c,梯子与地面的夹角为45°,将梯子顶端放于对面一堵墙上R点,离开地面的高度为d,此时梯子与地面的夹角为75°,则d=a,为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
| 日期 | 1日 | 2日 | 3日 | 4日 | 5日 | 6日 | 7日 |
| 人数变化 单位:万人 | +1.6 | +0.8 | +0.4 | -0.4 | -0.8 | +0.2 | -1.2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com