
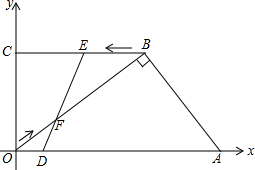
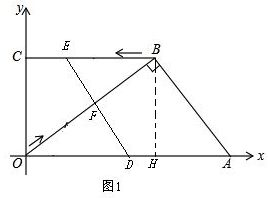
 如图,在平面直角坐标系中,A(
如图,在平面直角坐标系中,A(| 25 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
| 15 |
| 2 |
| 5 |
| 2 |
| 5 |
| 2 |
| OB |
| OA |
| OH |
| OB |
| 25 |
| 2 |
| 25 |
| 2 |
| 25 |
| 2 |
| OB2-OH2 |
| BF |
| OH |
| BE |
| OB |
10-
| ||
| 8 |
| ||
| 10 |
| 20 |
| 17 |
| 15 |
| 2 |
| 20 |
| 17 |
| 150 |
| 17 |
| 150 |
| 17 |
| 900 |
| 17 |
| 20 |
| 17 |
| 900 |
| 17 |
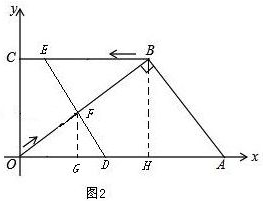 过点F作FG⊥OA于G,如图2,
过点F作FG⊥OA于G,如图2,| OG |
| OH |
| GF |
| HB |
| OF |
| OB |
| OG |
| 8 |
| GF |
| 6 |
| ||
| 10 |
| 3t |
| 2 |
| 3 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| 15 |
| 2 |
| k |
| x |
| 15 |
| 2 |
| 3 |
| 2 |
|
|
| 3 |
| x |


科目:初中数学 来源: 题型:
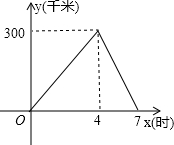 小李从甲地前往乙地,到达乙地后立刻返回,他与甲地的距离y(千米)与所用时间x(时)的函数关系如图所示.
小李从甲地前往乙地,到达乙地后立刻返回,他与甲地的距离y(千米)与所用时间x(时)的函数关系如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:
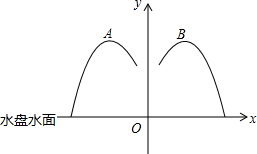 一个台型喷泉,若沿着中轴线截面,得到如图所示的抛物线,一个单位长度是1米,已知这两段抛物线关于y轴对称,其右侧的抛物线为:y=-4x2+4x(
一个台型喷泉,若沿着中轴线截面,得到如图所示的抛物线,一个单位长度是1米,已知这两段抛物线关于y轴对称,其右侧的抛物线为:y=-4x2+4x(| 1 |
| 8 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com