
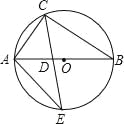
【题目】如图,△ABC内接于⊙O,AB是⊙O的直径,∠B=30°,CE平分∠ACB交⊙O于E,交AB于点D,连接AE,则S△ADE:S△CDB的值等于( )
A. 1:![]() B. 1:
B. 1:![]() C. 1:2 D. 2:3
C. 1:2 D. 2:3
【答案】D
【解析】
试题由AB是⊙O的直径,得到∠ACB=90°,根据已知条件得到![]() ,根据三角形的角平分线定理得到
,根据三角形的角平分线定理得到![]() ,求出AD=
,求出AD=![]() AB,BD=
AB,BD=![]() AB,过C作CE⊥AB于E,连接OE,由CE平分∠ACB交⊙O于E,得到OE⊥AB,求出OE=
AB,过C作CE⊥AB于E,连接OE,由CE平分∠ACB交⊙O于E,得到OE⊥AB,求出OE=![]() AB,CE=
AB,CE=![]() AB,根据三角形的面积公式即可得到结论.
AB,根据三角形的面积公式即可得到结论.
∵AB是⊙O的直径, ∴∠ACB=90°,∵∠B=30°,∴![]() ,
,
∵CE平分∠ACB交⊙O于E,∴![]() ,∴AD=
,∴AD=![]() AB,BD=
AB,BD=![]() AB,
AB,
过C作CE⊥AB于E,连接OE,∵CE平分∠ACB交⊙O于E,∴![]() =
=![]() ,
,
∴OE⊥AB,∴OE=![]() AB,CE=
AB,CE=![]() AB,
AB,
∴S△ADE:S△CDB=(![]() AD`OE):(
AD`OE):(![]() BD`CE)=(
BD`CE)=(![]() ×
×![]() AB·
AB·![]() AB):(
AB):(![]() ×
×![]() AB·
AB·![]() AB)=2:3.
AB)=2:3.



 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,直线l1:y=2x+1与直线l2:y=mx+4相交于点P(1,b)
(1)求b,m的值
(2)垂直于x轴的直线x=a与直线l1,l2分别相交于C,D,若线段CD长为2,求a的值

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了迎接“炎帝故里寻根节”,某校开展了主题为“炎帝文化知多少”的专题调查活动,采取随机抽样的方式进行问卷调查,问卷调查的结果分为“非常了解”“比较了解”“基本了解”“不太了解”四个等级,整理调查数据制成了下面的表格和如图所示的不完整的扇形统计图.
等级 | 非常了解 | 比较了解 | 基本了解 | 不太了解 |
频数 | 50 | m | 40 | 20 |

根据以上提供的信息,解答下列问题:
(1)本次问卷调查共抽取的学生人数为________,表中m的值为________;
(2)计算等级为“非常了解”的频数在扇形统计图中对应扇形的圆心角的度数,并补全扇形统计图;
(3)若该校有学生1 500人,请根据调查结果估计这些学生中“不太了解”炎帝文化知识的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 已知,反比例函数y=![]() 的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
的图象和一次函数的图象交于A、B两点,点A的横坐标是-1,点B的纵坐标是-1.
(1)求这个一次函数的表达式;
(2)若点P(m,n)在反比例函数图象上,且点P关于x轴对称的点Q恰好落在一次函数的图象上,求m2+n2的值;
(3)若M(x1,y1),N(x2,y2)是反比例函数在第一象限图象上的两点,满足x2-x1=2,y1+y2=3,求△MON的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于点
轴交于点![]() ,点
,点![]() 是反比例函数
是反比例函数![]() 的图象上位于直线
的图象上位于直线![]() 下方的点,过点
下方的点,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足分别为点
轴的垂线,垂足分别为点![]() ,交直线
,交直线![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() 的值为__________.
的值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明袋子中有1个红球和n个白球,这些球除颜色外无其他差别.
(1)当n=l时,从袋中随机摸出1个球,摸到红球与摸到白球的可能性是否相同? (填“相同”或“不相同”)
(2)从袋中随机摸出1个球,记录其颜色,然后放回,大量重复该实验,发现摸到红球的频率稳定于0.25,则n的值是 ;
(3)当n=2时,请用列表或画树状图的方法求两次摸出的球颜色不同的概率(摸出一个球,不放回,然后再摸一个球).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() (
(![]() 为常数)
为常数)
(1)该函数的图像与![]() 轴公共点的个数是( )
轴公共点的个数是( )
A.0 B.1 C.2 D.1或2
(2)求证:不论![]() 为何值,该函数的图像的顶点都在函数
为何值,该函数的图像的顶点都在函数![]() 的图像上.
的图像上.
(3)当![]() 时,求该函数的图像的顶点纵坐标的取值范围.
时,求该函数的图像的顶点纵坐标的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的四个角向内折起,恰好拼成一个无缝隙无重叠的四边形EFGH,EH=12厘米,EF=16厘米,则边AD的长是( )

A. 12厘米 B. 16厘米 C. 20厘米 D. 28厘米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于等腰三角形,以下说法正确的是( )
A.有一个角为40°的等腰三角形一定是锐角三角形
B.等腰三角形两边上的中线一定相等
C.两个等腰三角形中,若一腰以及该腰上的高对应相等,则这两个等腰三角形全等
D.等腰三角形两底角的平分线的交点到三边距离相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com