
【题目】一个不透明袋子中有1个红球和n个白球,这些球除颜色外无其他差别.
(1)当n=l时,从袋中随机摸出1个球,摸到红球与摸到白球的可能性是否相同? (填“相同”或“不相同”)
(2)从袋中随机摸出1个球,记录其颜色,然后放回,大量重复该实验,发现摸到红球的频率稳定于0.25,则n的值是 ;
(3)当n=2时,请用列表或画树状图的方法求两次摸出的球颜色不同的概率(摸出一个球,不放回,然后再摸一个球).
【答案】(1)相同;(2)3;(3)![]() .
.
【解析】
试题分析:(1)n=1,袋子中有1个红球和1个白球,则从袋中随机摸出1个球,摸到红球与摸到白球的概率都为![]() ;
;
(2)利用频率估计概率得到摸到红球的概率为0.25,则根据概率公式得到![]() =0.25,然后解方程即可;
=0.25,然后解方程即可;
(3)当n=2时,即不透明袋子中有1个红球和2个白球,画树状图展示所有6种等可能的结果数,找出两次摸出的球颜色不同的结果数,然后根据概率公式求解.
解:(1)当n=l时,从袋中随机摸出1个球,摸到红球与摸到白球的可能性相同;
(2)根据题意,估计摸到红球的概率为0.25,
所以![]() =0.25,解得n=3;
=0.25,解得n=3;
故答案为:相同,3;
(3)当n=2时,即不透明袋子中有1个红球和2个白球,
画树状图为:
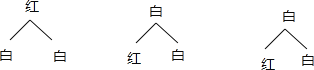
共有6种等可能的结果数,其中两次摸出的球颜色不同的结果数为4,
所以两次摸出的球颜色不同的概率=![]() =
=![]() .
.


 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
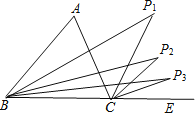
【题目】如图,已知∠A=n°,若P1点是∠ABC和外角∠ACE的角平分线的交点,P2点是∠P1BC和外角∠P1CE的角平分线的交点,P3点是∠P2BC和外角∠P2CE的交点…依此类推,则∠Pn=( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三角形纸片内有100个点,连同三角形的顶点共103个点,其中任意三点都不共线.现以这些点为顶点作三角形,并把纸片剪成小三角形,这样的小三角形的个数是( )
A. 299 B. 201 C. 205 D. 207
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线PA是一次函数y=x+1的图象,直线PB是一次函数y=﹣2x+2的图象.

(1)求A、B、P三点的坐标;
(2)求四边形PQOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知⊙O是Rt△ABC的外接圆,∠ACB=90°,AC平分∠BAD,CD⊥AD于D,AD交⊙O于E.
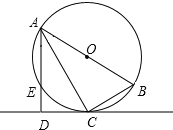
(1)求证:CD为⊙O的切线;
(2)若⊙O的直径为8cm,CD=2![]() cm,求弦AE的长.
cm,求弦AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中真命题是( )
A. 同位角相等 B. 在同一平面内,如果a⊥b,b⊥c,则a⊥c
C. 相等的角是对顶角 D. 在同一平面内,如果a∥b,b∥c,则a∥c
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com