
����Ŀ���ţ�1������ѧ��ȤС�龭���г����飬������ij����Ʒ�ڵ�x��1��x��90������ۼ����������������Ϣ���±���
ʱ��x���죩 | 1��x��50 | 50��x��90 |
�ۼۣ�Ԫ/���� | x+40 | 90 |
ÿ������������ | 200��2x | 200��2x |
��֪����Ʒ�Ľ���Ϊÿ��30Ԫ�������۸���Ʒ��ÿ������ΪyԪ
��1�����y��x�ĺ�����ϵʽ��
��2�������۸���Ʒ�ڼ���ʱ�������������������������Ƕ��٣�
��3������Ʒ�����۹����У����ж�����ÿ������������4800Ԫ����ֱ��д�������
���𰸡���1��y��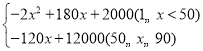 ����2��45��ʱ�����������6050Ԫ����3��41�죮
����2��45��ʱ�����������6050Ԫ����3��41�죮
��������
��1�����ݵ��۳����������ɵ����ɵ�y��x�ĺ�����ϵʽ��
��2�����ݷֶκ��������ʣ��ɷֱ�ó����ֵ�������������ıȽϣ��ɵô𰸣�
��3�����ݶ��κ���ֵ���ڻ����4800��һ�κ���ֵ���ڻ����48000���ɵò���ʽ�����ݽⲻ��ʽ�飬�ɵô𰸣�
�⣺��1����1��x��50ʱ��y����200��2x����x+40��30������2x2+180x+2000��
��50��x��90ʱ��
y����200��2x����90��30������120x+12000��
����������y�� ��
��
��2����1��x��50ʱ��
y����2x2+180x+2000��
y����2��x��45��2+6050��
��a����2��0��
����κ��������£����κ����Գ���Ϊx��45��
��x��45ʱ��y���6050��
��50��x��90ʱ��y��x���������С��
��x��50ʱ��y���6000��
��������������Ʒ��45��ʱ��������������������������6050Ԫ��
��3���ٵ�1��x��50ʱ��y����2x2+180x+2000��4800��
��ã�20��x��70��
���������4800Ԫ��������20��x��50����30�죻
�ڵ�50��x��90ʱ��y����120x+12000��4800��
��ã�x��60��
���������4800Ԫ��������50��x��60����11�죬
���Ը���Ʒ���������۹����У���41��ÿ������������4800Ԫ��


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ѧ�оŰٶ���ʦ������μ����ʵ���������ij�ֿͳ������������ÿ�����պ���������ÿ���˶��պ���һ����λ�����ͻ�����14���ˣ��������һ��������ôÿ�����պö���1����λ�������ֿͳ�ÿ���ij˿���λ��_____����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪����ABCD��һ���ڽǡ�BAD=80�����Խ���AC��BD�ཻ�ڵ�O����E��AB�ϣ���BE=BO�����EOA=___________��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij��ҵ�����һ���Ʒ��ÿ���ijɱ���50Ԫ��Ϊ�˺������ۣ�Ͷ���г��������������г����飬���۵�����100Ԫʱ��ÿ�����������50���������۵���ÿ����1Ԫ��ÿ��Ϳɶ��۳�5������Ҫ�����۵��۲��õ��ڳɱ�
��1����ÿ�����������y��Ԫ�������۵���x��Ԫ��֮��ĺ�����ϵʽ��
��2��������۵���Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
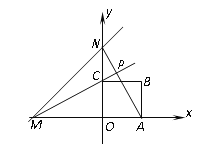
����Ŀ��ֱ��![]() �ֱ���x�ᡢy���ཻ���M��N���߳�Ϊ2��������OABCһ������O������ϵ��ԭ�㣬ֱ��AN��MC�ཻ���P�������������ŵ�O��תһ�ܣ����P���㣨0��2�����ȵ���Сֵ�ǣ� ��
�ֱ���x�ᡢy���ཻ���M��N���߳�Ϊ2��������OABCһ������O������ϵ��ԭ�㣬ֱ��AN��MC�ཻ���P�������������ŵ�O��תһ�ܣ����P���㣨0��2�����ȵ���Сֵ�ǣ� ��
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У���һ�麬��
�У���һ�麬��![]() �ǵ�ֱ�����ǰ���ͼ���ã�ֱ�Ƕ���
�ǵ�ֱ�����ǰ���ͼ���ã�ֱ�Ƕ���![]() ������Ϊ
������Ϊ![]() ������
������![]() ������Ϊ
������Ϊ![]() ������
������![]() ǡ�����ڵ�һ����˫�����ϣ��ֽ�ֱ�����ǰ���
ǡ�����ڵ�һ����˫�����ϣ��ֽ�ֱ�����ǰ���![]() ��������ƽ�ƣ�������
��������ƽ�ƣ�������![]() ǡ�����ڸ�˫������ʱֹͣ�˶������ʱ��
ǡ�����ڸ�˫������ʱֹͣ�˶������ʱ��![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ������Ϊ�� ��
�������� ��
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
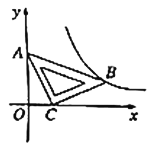
����Ŀ����ͼ��������![]() ��ͼ�����
��ͼ�����![]() .
.
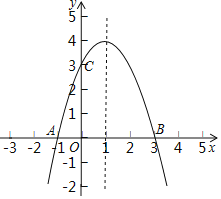
��1���������ߵĽ���ʽ��
��2���������ߵĶԳ������Ƿ����һ��P��ʹ�á�PAC���ܳ���С�������ڣ��������P�����꼰��PAC���ܳ����������ڣ���˵�����ɣ�
��3���ڣ�2���������£���x���Ϸ������������Ƿ���ڵ�M������C���غϣ���ʹ��![]() �������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
�������ڣ��������M�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У�BC=4��AB=3��������B�͵�D��������Բ����AC���У�����AB��BC��AD��DC�ֱ��ڵ�G��H��E��F����EF+GH����Сֵ�ǣ� ��
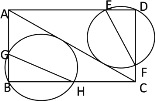
A.3B.4C.4.8D.5
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
��![]() ��
��![]() ��
��![]() ��
��![]() ��һ�㣬
��һ�㣬![]() ��
��![]() ��
��![]() ����һ���㣬���ı���
����һ���㣬���ı���![]() ��ֱ��
��ֱ��![]() �۵���
�۵���![]() �Ķ�Ӧ��
�Ķ�Ӧ��![]() ����
����![]() �ij�����Сʱ����
�ij�����Сʱ����![]() �ij�Ϊ_______
�ij�Ϊ_______
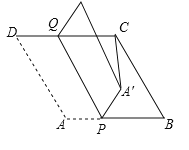
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com