
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑到学校.如果小明跑步的速度均匀的,到达小彬家用了8分钟,整个跑步过程用时共32分钟.
(1)以小明家为原点、向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家;
(2)用点C表示出学校的位置;
(3)求小彬家与学校之间的距离.
![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,A,B,C,D为矩形的四个顶点,AB=16 cm,BC=6 cm,动点P,Q分别从点A,C同时出发,点P以3 cm/s的速度向点B移动,点Q以2 cm/s的速度向点D移动.当点P运动到点B停止时,点Q也随之停止运动.问几秒时点P和点Q的距离是10 cm?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明:
如图,已知∠1、∠2互为补角,且∠3=∠B,
求证:∠AED=∠ACB.
证明:∵∠1+∠2=180°,∠2+∠4=180°
∴∠1=∠4 (______)
∴AB∥EF(_______)
∴∠3=______(______)
又∠3=∠B
∴∠B=_______(_______)
∴DE∥BC (________)
∴∠AED=∠ACB (_______)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠C>∠B.如图①,AD⊥BC于点D,AE平分∠BAC.
(1)如图①,AD⊥BC于点D,AE平分∠BAC,能猜想出∠DAE与∠B、∠C之间的关系是什么?并说明理由.
(2)如图②,AE平分∠BAC,F为AE上的一点,且FD⊥BC于点D,这时∠EFD与∠B、∠C有何数量关系?请说明理由.
(3)如图③,AE平分∠BAC,F为AE延长线上的一点,FD⊥BC于点D,请你写出这时∠EFD与∠B、∠C之间的数量关系(只写结论,不必说明理由).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=_______________时,△ABC与△QPA全等.
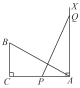
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O为直线AB上一点,过点O作射线OC,使∠AOC:∠BOC=2:1,将直角三角板的直角顶点放在点O处,一边ON在射线OA上,另一边OM在直线AB的下方.
(1)在图1中,∠AOC= °,∠MOC= °;
(2)将图1中的三角板按图2的位置放置,使得OM在射线QA上,求∠CON的度数;
(3)将上述直角三角板按图3的位置放置,OM在∠BOC的内部,说明∠BON﹣∠COM的值固定不变.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八(2)班组织了一次经典诵读比赛,甲、乙两队各10人的比赛成绩如下表(10分制):
甲 | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
乙 | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)甲队成绩的中位数是 分,乙队成绩的众数是 分;
(2)计算乙队的平均成绩和方差;
(3)已知甲队成绩的方差是1.4,则成绩较为整齐的是 队.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com