
【题目】在△ABC中,∠C>∠B.如图①,AD⊥BC于点D,AE平分∠BAC.
(1)如图①,AD⊥BC于点D,AE平分∠BAC,能猜想出∠DAE与∠B、∠C之间的关系是什么?并说明理由.
(2)如图②,AE平分∠BAC,F为AE上的一点,且FD⊥BC于点D,这时∠EFD与∠B、∠C有何数量关系?请说明理由.
(3)如图③,AE平分∠BAC,F为AE延长线上的一点,FD⊥BC于点D,请你写出这时∠EFD与∠B、∠C之间的数量关系(只写结论,不必说明理由).

【答案】(1)![]() ,证明详见解析;(2)
,证明详见解析;(2)![]() ,证明详见解析;(3)
,证明详见解析;(3)![]()
【解析】
(1)由图不难发现∠EAD=∠EAC-∠DAC,再根据三角形的内角和定理及其推论结合角平分线的定义分别用结论中出现的角替换∠EAC和∠DAC.
(2)由角平分线的性质和三角形的内角和得出∠BAE=90°-![]() (∠C+∠B),外角的性质得出∠AEC=90°+
(∠C+∠B),外角的性质得出∠AEC=90°+![]() (∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(∠B-∠C),在△EFD中,由三角形内角和定理可得∠EFD;
(3)与(2)的方法相同.
证明:(1)∵AE平分∠BAC,

∴∠BAE=∠CAE=![]() ∠BAC
∠BAC
∵∠BAC=180°-(∠B+∠C)
∴∠EAC=![]() [180°-(∠B+∠C)]
[180°-(∠B+∠C)]
∵AD⊥BC,
∴∠ADC=90°,
∴∠DAC=180°-∠ADC-∠C=90°-∠C,
∵∠EAD=∠EAC-∠DAC
∴∠EAD=![]() [180°-(∠B+∠C)]-(90°-∠C)=
[180°-(∠B+∠C)]-(90°-∠C)=![]() (∠C-∠B).
(∠C-∠B).
(2)∠EFD=![]() (∠C-∠B)
(∠C-∠B)
∵AE平分∠BAC,
∴∠BAE=![]() =90°-
=90°-![]() (∠C+∠B),
(∠C+∠B),
∵∠AEC为△ABE的外角,
∴∠AEC=∠B+90°-![]() (∠C+∠B)=90°+
(∠C+∠B)=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C)
(∠B-∠C)
∴∠EFD=![]() (∠C-∠B)
(∠C-∠B)
(3)∠EFD=![]() (∠C-∠B).
(∠C-∠B).
∵AE平分∠BAC,
∴∠BAE=![]() .
.
∵∠DEF为△ABE的外角,
∴∠DEF=∠B+![]() =90°+
=90°+![]() (∠B-∠C),
(∠B-∠C),
∵FD⊥BC,
∴∠FDE=90°.
∴∠EFD=90°-90°-![]() (∠B-∠C),
(∠B-∠C),
∴∠EFD=![]() (∠C-∠B).
(∠C-∠B).


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,Rt△ABC的顶点B在原点O,直角边BC在x轴的正半轴上,∠ACB=90°,点A的坐标为(3, ![]() ),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 .
),点D是BC边上一个动点(不与点B,C重合),过点D作DE⊥BC交AB边于点E,将∠ABC沿直线DE翻折,点B落在x轴上的点F处当△AEF为直角三角形时,点F的坐标是 . 
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块直角三角板![]() 放置在锐角
放置在锐角![]() 上,使得该三角板的两条直角边
上,使得该三角板的两条直角边![]() 恰好分别经过点
恰好分别经过点![]()
(1)如图①,若![]() 时,点
时,点![]() 在
在![]() 内,则
内,则![]() 度,
度,![]() ____度,
____度,![]() 度;
度;
(2)如图②,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 内,请探究
内,请探究![]() 与
与![]() 之间存在怎样的数量关系,并验证你的结论;
之间存在怎样的数量关系,并验证你的结论;
(3)如图③,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 外,且在
外,且在![]() 边的左侧,直接写出
边的左侧,直接写出![]() 三者之间存在的数量关系.
三者之间存在的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的10张卡片上分别写有11至20十个数字,将它们背面朝上洗匀后,任意抽一张,将下列事件发生的机会的大小填在横线上.
![]()
(1)P1(抽到数字11)=_______;
(2)P2(抽到两位数)=_______,P3(抽到一位数)=_______;
(3)P4(抽到的数大于10)=_______,P5(抽到的数大于16)=_______,P6(抽到的数小于16)=_______;
(4)P7(抽到的数是2的倍数)=_______,P8(抽到的数是3的倍数)=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,点P是弦BC上一动点(不与B,C重合),过点P作PE⊥AB,垂足为E,在射线EP上取点D使得DC=DP,连接DC.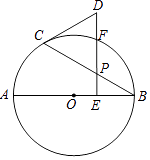
(1)求证:DC是⊙O的切线;
(2)若∠CBA=30°,射线EP交⊙O于点 F,当点 F恰好是弧BC的中点时,判断以B,O,C,F为顶点的四边形是什么特殊四边形?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的平分线BE交AD于点F,则图中共有等腰三角形( )
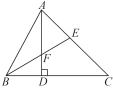
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明早晨跑步,他从自己家出发,向东跑了2km到达小彬家,继续向东跑了1.5km到达小红家,然后又向西跑到学校.如果小明跑步的速度均匀的,到达小彬家用了8分钟,整个跑步过程用时共32分钟.
(1)以小明家为原点、向东为正方向,用1个单位长度表示1km,在图中的数轴上,分别用点A表示出小彬家,用点B表示出小红家;
(2)用点C表示出学校的位置;
(3)求小彬家与学校之间的距离.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等腰△ABC中,AB=AC,点D在AC边上,点E在BC边上,且∠AED=∠B,若AB=10,BE=5,AE=2 ![]() ,则线段CE的长为( )
,则线段CE的长为( ) 
A.![]()
B.8
C.2 ![]()
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A城有某种农机30台,B城有该农机40台,现要将这些农机全部运往C,D两乡,调运任务承包给某运输公司.已知C乡需要农机34台,D乡需要农机36台,从A城往C,D两乡运送农机的费用分别为250元/台和200元/台,从B城往C,D两乡运送农机的费用分别为150元/台和240元/台.
(1)设A城运往C乡该农机x台,运送全部农机的总费用为W元,求W关于x的函数关系式,并写出自变量x的取值范围.
(2)现该运输公司要求运送全部农机的总费用不低于16460元,则有多少种不同的调运方案?将这些方案设计出来.
(3)现该运输公司决定对A城运往C乡的农机,从运输费中每台减免a元(a≤200)作为优惠,其他费用不变,如何调运,使总费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com