Question

【题目】如图，AB是⊙O的直径，点P是弦BC上一动点（不与B，C重合），过点P作PE⊥AB，垂足为E，在射线EP上取点D使得DC=DP，连接DC．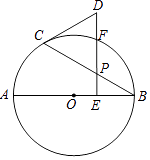

（1）求证：DC是⊙O的切线；
（2）若∠CBA=30°，射线EP交⊙O于点 F，当点 F恰好是弧BC的中点时，判断以B，O，C，F为顶点的四边形是什么特殊四边形？说明理由．

Answer 1

【答案】
（1）证明：连接OC，

∵DP=DC，

∴∠DPC=∠DCP，

∵∠DPC=∠BPE，

∴∠BPE=∠DCP，

∵PE⊥AB，

∴∠BEP=90°，

∴∠B+∠APE=90°，

∵OB=OC，

∴∠OCB=∠B，

∴∠OCB+∠DCP=90°，

∴OC⊥CD，

∴直线CD与⊙O相切

（2）解：以B、O、C、F为顶点的四边形是菱形，理由如下：

连接AC，

∵∠CBA=30°，

∴∠A=60°，

∴△OAC为等边三角形，

∴∠BOC=120°，

连接OF，BF，CF

∵F是弧BC的中点，

∴∠BOF=∠COF=60°，

∴△BOF与△COF均为等边三角形，

∴BF=BO=OC=CF，

∴四边形BOCF为菱形．

【解析】（1）连接OC，然后依据已知条件和圆的基本性质证明OC⊥CD，最后，依据切线的判定定理进行证明即可；
（2）连接AC，由∠CAB=30°可证明△OAC为等边三角形，于是可得到∠BOC=120°，由F是弧AC的中点，易证明△BOF、△COF均为等边三角形，依据等边三角形的性质可得到BF=BO=OC=CF，从而可证明四边形BOCF为菱形.

【考点精析】根据题目的已知条件，利用菱形的判定方法的相关知识可以得到问题的答案，需要掌握任意一个四边形，四边相等成菱形；四边形的对角线，垂直互分是菱形．已知平行四边形，邻边相等叫菱形；两对角线若垂直，顺理成章为菱形．