
����Ŀ��A����ij��ũ��30̨,B���и�ũ��40̨,��Ҫ����Щũ��ȫ������C,D����,��������а���ij���乫˾.��֪C����Ҫũ��34̨,D����Ҫũ��36̨,��A����C,D��������ũ���ķ��÷ֱ�Ϊ250Ԫ/̨��200Ԫ/̨,��B����C,D��������ũ���ķ��÷ֱ�Ϊ150Ԫ/̨��240Ԫ/̨.
(1)��A������C���ũ��x̨,����ȫ��ũ�����ܷ���ΪWԪ,��W����x�ĺ�����ϵʽ,��д���Ա���x��ȡֵ��Χ.
(2)�ָ����乫˾Ҫ������ȫ��ũ�����ܷ��ò�����16460Ԫ,���ж����ֲ�ͬ�ĵ��˷���?����Щ������Ƴ���.
(3)�ָ����乫˾������A������C���ũ��,���������ÿ̨����aԪ(a��200)��Ϊ�Ż�,�������ò���,��ε���,ʹ�ܷ�������?
���𰸡���1��W=140x+12540��0��x��30������2����3�ֲ�ͬ�ĵ��˷������������������3����A�ǵ���C��30̨������D��0̨���ӣ�B�ǵ���C��4̨������D��36̨��
��������
��1��A������C��Ļ���Ϊx�֣���ɵ�A������D��Ļ���Ϊ30-x�֣�B������C��Ļ���Ϊ34-x�֣�B������D��Ļ���Ϊ40-��34-x���֣��Ӷ��ɵó�W��x��ĺ�����ϵ��
��2�����������140x+12540��16460���28��x��30�����ǵõ���3�ֲ�ͬ�ĵ��˷�����д���������ɣ�
��3����������õ�W=��140-a��x+12540�����Ե�a=200ʱ��y=-60x+12540����ʱx=30ʱ��![]() =10740Ԫ�����ǵõ����ۣ�
=10740Ԫ�����ǵõ����ۣ�
���������
��1��W=250x+200��30��x��+150��34��x��+240��6+x��=140x+12540��0��x��30����
��2�����������140x+12540��16460����x��28��
��x��30����28��x��30������3�ֲ�ͬ�ĵ��˷�����
��һ�ֵ��˷�������A�ǵ���C��28̨������D��2̨���ӣ�B�ǵ���C��6̨������D��34̨��
�ڶ��ֵ��˷�������A�ǵ���C��29̨������D��1̨���ӣ�B�ǵ���C��5̨������D��35̨��
�����ֵ��˷�������A�ǵ���C��30̨������D��0̨���ӣ�B�ǵ���C��4̨������D��36̨��
��3��W=x+200��30��x��+150��34��x��+240��6+x��=x+12540��
���Ե�a=200ʱ��y��С=��60x+12540����ʱx=30ʱy��С=10740Ԫ��
��ʱ�ķ���Ϊ����A�ǵ���C��30̨������D��0̨���ӣ�B�ǵ���C��4̨������D��36̨��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
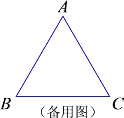
����Ŀ������ABC�У���C>��B����ͼ�٣�AD��BC�ڵ�D��AEƽ�֡�BAC��
��1����ͼ�٣�AD��BC�ڵ�D��AEƽ�֡�BAC���ܲ������DAE���B����C֮��Ĺ�ϵ��ʲô����˵�����ɣ�
��2����ͼ�ڣ�AEƽ�֡�BAC��FΪAE�ϵ�һ�㣬��FD��BC�ڵ�D����ʱ��EFD���B����C�к�������ϵ����˵�����ɣ�
��3����ͼ�ۣ�AEƽ�֡�BAC��FΪAE�ӳ����ϵ�һ�㣬FD��BC�ڵ�D������д����ʱ��EFD���B����C֮���������ϵ(ֻд���ۣ�����˵������)��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
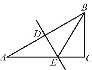
����Ŀ����ͼ����Rt��ABC�У���C=90������ABC=60����AB�Ĵ�ֱƽ���߷ֱ�AB��AC�ڵ�D�͵�E.��CE=2����AB�ij���_____.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��AB��CD�ཻ�ڵ�O��OF��OD�ֱ��ǡ�AOE����BOE��ƽ���ߣ�
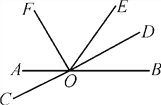
(1)д����DOE�IJ��ǣ�
(2)����BOE��62�㣬���AOD�͡�EOF�Ķ�����
(3)��������OD��OF֮����ʲô�����λ�ù�ϵ��Ϊʲô��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AE�ǡ�ACD�Ľ�ƽ���ߣ�B��DA�ӳ����ϣ�AE��BC��FΪBC�е㣬�ж�AE��AF��λ�ù�ϵ��֤��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1����ʦ�ڿ��ϸ���������һ����Ŀ����ͼ��1�����ȱߡ�ABC�߳�Ϊ2����AB����һ��P��PE��AC��E��QΪBC�ӳ�����һ�㣬��AP=CQ������PQ��AC��D����DE�ij�.
С��ͬѧ��������˼������Ϊ������ͨ������P��ƽ���߹���ȱ������εķ���������������.�����С��ͬѧ��˼·ֱ��д��DE�ij�.
��2�������̽����
��ʦ����ͬѧ�����о���
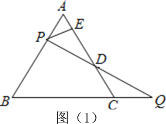
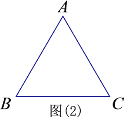
�ٵȱߡ�ABC�߳�Ϊ2����PΪBA���ӳ�����һ��ʱ,��PE��CA���ӳ����ڵ�E ��QΪ��BC��һ�㣬��AP=CQ������PQ��AC��D.������ͼ��2���в�ȫͼ�β���DE�ij�.
����֪�ȱߡ�ABC����PΪAB���ӳ�����һ��ʱ,��PE������AC�ڵ�E�� QΪ��һ������BC���ϣ���BC���ӳ����ϣ���CB���ӳ����ϣ�һ�㣬��AP=CQ������PQ��ֱ��AC�ڵ�D����ʹ��DE�ij��ȱ��ֲ���.( ֱ��д���𰸵ı��)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����(2)����֯��һ�ξ����ж��������ס������Ӹ�10�˵ı����ɼ����±�(10����)��
�� | 7 | 8 | 9 | 7 | 10 | 10 | 9 | 10 | 10 | 10 |
�� | 10 | 8 | 7 | 9 | 8 | 10 | 10 | 9 | 10 | 9 |
(1)�ӳɼ�����λ���� �֣��Ҷӳɼ��������� �֣�
(2)�����Ҷӵ�ƽ���ɼ��ͷ��
(3)��֪�ӳɼ��ķ�����1.4����ɼ���Ϊ������� �ӣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ�����κ���y=ax2+bx+c��a��0����ͼ����x�ύ��A��3��0����B����1��0�����㣬��y���ཻ�ڵ�C��0����3��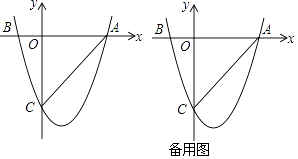
��1����ö��κ����Ľ���ʽ��
��2����E��y���Ҳ������������ڵ�A��һ�����㣬����E��x���ƽ���߽�����������һ��F������F��FG��ֱ��x���ڵ�G���ٹ���E��EH��ֱ��x���ڵ�H���õ�����EFGH�����ڵ�E���˶������У�������EFGHΪ������ʱ������������εı߳���
��3����P����x���·����������ϵ�һ�����㣬����PA��PC�����PAC�����ȡֵ��Χ������PAC���Ϊ����ʱ�������ġ�PAC�м�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ཫ����֪ʶ������������С������Ʒ��С��ȥ�Ļ���Ʒ���������ִ�С��ͬ�ıʼDZ�һ��a�������д�ʼDZ�����8Ԫ��С�ʼDZ�����5Ԫ��������5ԪС�ʼDZ�����x����
��1��������
���ۣ�Ԫ/���� | ���������� | ��Ԫ�� | |
С�ʼDZ� | 5 | x | 5x |
��ʼDZ� | 8 |
��2����ʽ��ʾ��С�����С�ʼDZ����� Ԫ��
��3����С���Ӱ��������300Ԫ������40����С��ͬ�����ֱʼDZ�(a��40)�����һ�55Ԫ�������ôС�����˴�С�ʼDZ������ٱ���
��4����������´λ�У���С���պû�400Ԫ���������ִ�С�ʼDZ������ҹ����С�ʼDZ�����xҪС��60��������Ҫ����30��(30��x��60)�����о�С���п��ܹ���ķ�������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com