
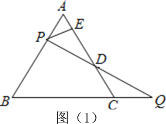
ЁОЬтФПЁПЃЈ1ЃЉРЯЪІдкПЮЩЯИјГіСЫетбљвЛЕРЬтФПЃКШчЭМЃЈ1ЃЉЃЌЕШБпЁїABCБпГЄЮЊ2ЃЌЙ§ABБпЩЯвЛЕуPзїPEЁЭACгкEЃЌQЮЊBCбгГЄЯпЩЯвЛЕуЃЌЧвAP=CQЃЌСЌНгPQНЛACгкDЃЌЧѓDEЕФГЄ.
аЁУїЭЌбЇОЙ§ШЯецЫМПМКѓШЯЮЊЃЌПЩвдЭЈЙ§Й§ЕуPзїЦНааЯпЙЙдьЕШБпШ§НЧаЮЕФЗНЗЈРДНтОіетИіЮЪЬт.ЧыИљОнаЁУїЭЌбЇЕФЫМТЗжБНгаДГіDEЕФГЄ.
ЃЈ2ЃЉЃЈРрБШЬНОПЃЉ
РЯЪІв§ЕМЭЌбЇМЬајбаОПЃК
ЂйЕШБпЁїABCБпГЄЮЊ2ЃЌЕБPЮЊBAЕФбгГЄЯпЩЯвЛЕуЪБ,зїPEЁЭCAЕФбгГЄЯпгкЕуE ЃЌQЮЊБпBCЩЯвЛЕуЃЌЧвAP=CQЃЌСЌНгPQНЛACгкD.ЧыФудкЭМЃЈ2ЃЉжаВЙШЋЭМаЮВЂЧѓDEЕФГЄ.
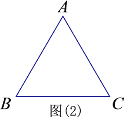
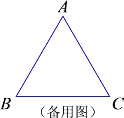
ЂквбжЊЕШБпЁїABCЃЌЕБPЮЊABЕФбгГЄЯпЩЯвЛЕуЪБ,зїPEЁЭЩфЯпACгкЕуEЃЌ QЮЊФФвЛИіЃЈЂйBCБпЩЯЃЛЂкBCЕФбгГЄЯпЩЯЃЛЂлCBЕФбгГЄЯпЩЯЃЉвЛЕуЃЌЧвAP=CQЃЌСЌНгPQНЛжБЯпACгкЕуDЃЌФмЪЙЕУDEЕФГЄЖШБЃГжВЛБф.( жБНгаДГіД№АИЕФБрКХ)
ЁОД№АИЁПЃЈ1ЃЉDE=1ЃЛ(2) Ђйе§ШЗВЙШЋЭМаЮМћНтЮіЃЌЂк Ђк.
ЁОНтЮіЁП
ЃЈ1ЃЉЙ§PзїPFЁЮBCНЛACгкFЃЌЕУГіЕШБпШ§НЧаЮAPFЃЌЭЦГіAP=PF=QCЃЌИљОнЕШбќШ§НЧаЮаджЪЧѓГіEF=AEЃЌжЄЁїPFDЁеЁїQCDЃЌЭЦГіFD=CDЃЌЭЦГіDE![]() ACМДПЩЃЛ
ACМДПЩЃЛ
ЃЈ2ЃЉЂйЙ§ЕуPзїPFЁЮBCНЛCAЕФбгГЄЯпгыЕуFЃЌгЩЦНааЯпЕФаджЪЕУГіЁЯPFA=ЁЯCЃЎ
дйжЄУїЁїAPFЮЊЕШБпШ§НЧаЮЃЌЕУЕНAP=PFЃЎНјвЛВНЕУЕНAE=FE=![]() ЃЎгЩSASжЄУїЁїFDPЁеЁїCDQЃЌЕУЕНFD=CD=
ЃЎгЩSASжЄУїЁїFDPЁеЁїCDQЃЌЕУЕНFD=CD=![]() ЃЌИљОнЯпЖЮЕФКЭВюМДПЩЕУЕННсТлЃЎ
ЃЌИљОнЯпЖЮЕФКЭВюМДПЩЕУЕННсТлЃЎ
ЂкШчЭМЃЌЙ§PзїжБЯпPFЁЮBCНЛжБЯпACгкFЃЌЭЈЙ§жЄУїЁїAPFЪЧЕШБпШ§НЧаЮЃЌЕУЕНAP=PFЃЎНјЖјЕУЕНEF=AE=![]() AFЃЎдйгЩЯпЖЮЕФКЭВюМДПЩЕУГіНсТлЃЎ
AFЃЎдйгЩЯпЖЮЕФКЭВюМДПЩЕУГіНсТлЃЎ
ЃЈ1ЃЉЙ§PзїPFЁЮBCНЛACгкFЃЎ
ЁпPFЁЮBCЃЌЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрЁЯPFD=ЁЯQCDЃЌЁїAPFЪЧЕШБпШ§НЧаЮЃЌЁрAP=PF=AFЃЎ
ЁпPEЁЭACЃЌЁрAE=EFЃЎ
ЁпAP=PFЃЌAP=CQЃЌЁрPF=CQЃЎ
дкЁїPFDКЭЁїQCDжаЃЌЁп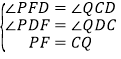 ЃЌЁрЁїPFDЁеЁїQCDЃЈAASЃЉЃЌЁрFD=CDЃЎ
ЃЌЁрЁїPFDЁеЁїQCDЃЈAASЃЉЃЌЁрFD=CDЃЎ
ЁпAE=EFЃЌЁрEF+FD=AE+CDЃЌЁрAE+CD=DE![]() ACЃЎ
ACЃЎ
ЁпAC=2ЃЌЁрDE=1ЃЎ
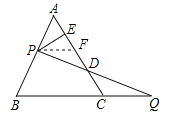
(2)Ђйе§ШЗВЙШЋЭМаЮЃЎ
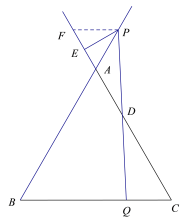
Й§ЕуPзїPFЁЮBCНЛCAЕФбгГЄЯпгыЕуFЃЌЁрЁЯPFA=ЁЯCЃЎ
ЁпЁїABCЪЧЕШБпШ§НЧаЮЃЌЁрЁЯBAC=ЁЯC=60ЁуЃЌЁрЁЯPFA=ЁЯPAF=60ЁуЃЌЁрЁїAPFЮЊЕШБпШ§НЧаЮЃЌЁрAP=PFЃЎ
гжЁпPEЁЭCAЕФбгГЄЯпгкЕуEЃЌЁрAE=FE=![]() ЃЎ
ЃЎ
ЁпAP=CQЃЌЁрPF=QCЃЎ
ЁпЁЯFDP=ЁЯCDQЃЌЁрЁїFDPЁеЁїCDQЃЌЁрFD=CD=![]() ЃЌЁрDE=DFЉEF=
ЃЌЁрDE=DFЉEF=![]() ЃЎ
ЃЎ
Ђк Д№АИЮЊЂкЃЎРэгЩШчЯТЃК
ШчЭМЃЌЙ§PзїжБЯпPFЁЮBCНЛжБЯпACгкFЃЌЁрЁЯAPF=ЁЯABC=60ЁуЃЎ
ЁпЁЯA=60ЁуЃЌЁрЁїAPFЪЧЕШБпШ§НЧаЮЃЌЁрAP=PFЃЎ
ЁпAP=CQЃЌЁрPF=QCЃЎ
ЁпPFЁЮBCЃЌЁрЁЯF=ЁЯDCQЃЌЁЯFPD=ЁЯQЃЎ
дкЁїDPFКЭЁїDQCжаЃЌЁпЁЯF=ЁЯDCQЃЌPF=QCЃЌЁЯFPD=ЁЯQЃЌЁрЁїDPFЁеЁїDQCЃЌЁрCD=DF=![]() CFЃЎ
CFЃЎ
ЁпЁїAPFЪЧЕШБпШ§НЧаЮЃЌPEЁЭAFЃЌЁрEF=AE=![]() AFЃЎ
AFЃЎ
ЁпED=EFЉDFЃЌЁрED=![]() AFЉ
AFЉ![]() CF=
CF=![]() ЃЈAFЉCFЃЉ=
ЃЈAFЉCFЃЉ=![]() ACЃЎ
ACЃЎ
ЁпACЕФГЄЖШВЛБфЃЌЁрDEЕФГЄЖШБЃГжВЛБфЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЁїABCжаЃЌЁЯABCЃН60ЁуЃЌЁЯCЃН45ЁуЃЌADЪЧBCБпЩЯЕФИпЃЌЁЯABCЕФЦНЗжЯпBEНЛADгкЕуFЃЌдђЭМжаЙВгаЕШбќШ§НЧаЮ( )
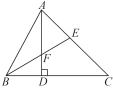
A. 2Иі B. 3Иі C. 4Иі D. 5Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
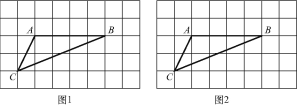
ЁОЬтФПЁПШчЭМ,дк8ЁС5ЕФе§ЗНаЮЭјИёжа,УПИіаЁе§ЗНаЮЕФБпГЄОљЮЊ1,ЁїABCЕФШ§ИіЖЅЕуОљдкаЁе§ЗНаЮЕФЖЅЕуЩЯ.
(1)дкЭМ1жаЛЁїABD(ЕуDдкаЁе§ЗНаЮЕФЖЅЕуЩЯ),ЪЙЁїABDЕФжмГЄЕШгкЁїABCЕФжмГЄ,ЧввдA,B,C,DЮЊЖЅЕуЕФЫФБпаЮЪЧжсЖдГЦЭМаЮ;
(2)дкЭМ2жаЛЁїABE(ЕуEдкаЁе§ЗНаЮЕФЖЅЕуЩЯ),ЪЙЁїABEЕФжмГЄЕШгкЁїABCЕФжмГЄ,ЧввдA,B,C,EЮЊЖЅЕуЕФЫФБпаЮЪЧжааФЖдГЦЭМаЮ,ВЂжБНгаДГіИУЫФБпаЮЕФУцЛ§.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПМЦЫуЃК|1Љ ![]() |+3tan30ЁуЉЃЈ
|+3tan30ЁуЉЃЈ ![]() Љ5ЃЉ0ЉЃЈЉ
Љ5ЃЉ0ЉЃЈЉ ![]() ЃЉЉ1 ЃЎ
ЃЉЉ1 ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПAГЧгаФГжжХЉЛњ30ЬЈ,BГЧгаИУХЉЛњ40ЬЈ,ЯжвЊНЋетаЉХЉЛњШЋВПдЫЭљC,DСНЯч,ЕїдЫШЮЮёГаАќИјФГдЫЪфЙЋЫО.вбжЊCЯчашвЊХЉЛњ34ЬЈ,DЯчашвЊХЉЛњ36ЬЈ,ДгAГЧЭљC,DСНЯчдЫЫЭХЉЛњЕФЗбгУЗжБ№ЮЊ250дЊ/ЬЈКЭ200дЊ/ЬЈ,ДгBГЧЭљC,DСНЯчдЫЫЭХЉЛњЕФЗбгУЗжБ№ЮЊ150дЊ/ЬЈКЭ240дЊ/ЬЈ.
(1)ЩшAГЧдЫЭљCЯчИУХЉЛњxЬЈ,дЫЫЭШЋВПХЉЛњЕФзмЗбгУЮЊWдЊ,ЧѓWЙигкxЕФКЏЪ§ЙиЯЕЪН,ВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇ.
(2)ЯжИУдЫЪфЙЋЫОвЊЧѓдЫЫЭШЋВПХЉЛњЕФзмЗбгУВЛЕЭгк16460дЊ,дђгаЖрЩйжжВЛЭЌЕФЕїдЫЗНАИ?НЋетаЉЗНАИЩшМЦГіРД.
(3)ЯжИУдЫЪфЙЋЫООіЖЈЖдAГЧдЫЭљCЯчЕФХЉЛњ,ДгдЫЪфЗбжаУПЬЈМѕУтaдЊ(aЁм200)зїЮЊгХЛн,ЦфЫћЗбгУВЛБф,ШчКЮЕїдЫ,ЪЙзмЗбгУзюЩй?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЁїABCКЭЁїADEЖМЪЧЕШбќжБНЧШ§НЧаЮЃЌЁЯBACЃНЁЯDAEЃН90ЁуЃЌСЌНсCEНЛADгкЕуFЃЌСЌНсBDНЛCEгкЕуGЃЌСЌНсBE.ЯТСаНсТлЃКЂйCEЃНBDЃЛЂкЁїADCЪЧЕШбќжБНЧШ§НЧаЮЃЛЂлЁЯADBЃНЁЯAEBЃЛЂмSЫФБпаЮBCDEЃН![]() BDЁЄCEЃЛЂнBC2ЃЋDE2ЃНBE2ЃЋCD2.Цфжае§ШЗЕФНсТлга( )
BDЁЄCEЃЛЂнBC2ЃЋDE2ЃНBE2ЃЋCD2.Цфжае§ШЗЕФНсТлга( )
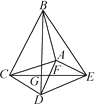
A. 1Иі B. 2Иі C. 3Иі D. 4Иі
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкRt![]() жаЃЌ
жаЃЌ![]() ЃЌЗжБ№вдЕуAЁЂCЮЊдВаФЃЌДѓгк
ЃЌЗжБ№вдЕуAЁЂCЮЊдВаФЃЌДѓгк![]() ГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуMЁЂNЃЌСЌНсMNЃЌгыACЁЂBCЗжБ№НЛгкЕуDЁЂEЃЌСЌНсAEЃЎ
ГЄЮЊАыОЖЛЛЁЃЌСНЛЁЯрНЛгкЕуMЁЂNЃЌСЌНсMNЃЌгыACЁЂBCЗжБ№НЛгкЕуDЁЂEЃЌСЌНсAEЃЎ
ЃЈ1ЃЉЧѓ![]() ЃЛЃЈжБНгаДГіНсЙћЃЉ
ЃЛЃЈжБНгаДГіНсЙћЃЉ
ЃЈ2ЃЉЕБAB=3ЃЌAC=5ЪБЃЌЧѓ![]() ЕФжмГЄЃЎ
ЕФжмГЄЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
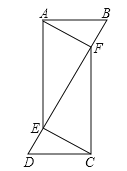
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЕуEЁЂFдкЯпЖЮBDЩЯЃЌAB=CDЃЌЁЯB=ЁЯDЃЌBF=DEЃЎ
ЧѓжЄЃКЃЈ1ЃЉAE=CFЃЛЃЈ2ЃЉAFЁЮCEЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDЖдНЧЯпBDЩЯНиШЁBE=BCЃЌСЌНгCEВЂбгГЄНЛADгкЕуFЃЌСЌНгAEЃЌЙ§BзїBGЁЭAEгкЕуGЃЌНЛADгкЕуHЃЌдђЯТСаНсТлДэЮѓЕФЪЧЃЈЁЁЁЁЃЉ
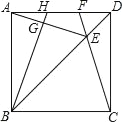
A. AH=DF B. SЫФБпаЮEFHG=SЁїDCF+SЁїAGH
C. ЁЯAEF=45Ёу D. ЁїABHЁеЁїDCF
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com