
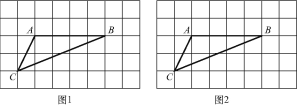
【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A,B,C,D为顶点的四边形是轴对称图形;
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A,B,C,E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
科目:初中数学 来源: 题型:
【题目】初二年级教师对试卷讲评课中学生参与情况进行调查,调查项目分为主动质疑、独立思考、专注听讲、讲解题目四项.调查组随机抽取了若干名初中学生的参与情况,绘制了如图所示的扇形统计图和条形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为______度;
(2)请将频数分布直方图补充完整;
(3)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
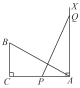
【题目】如图,∠C=90°,AC=10,BC=5,AX⊥AC,点P和点Q从A点出发,分别在线段AC和射线AX上运动,且AB=PQ,当点P运动到AP=_______________时,△ABC与△QPA全等.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角梯形AOCD的边OC在x轴上,O为坐标原点,CD垂直于x轴,D(5,4),AD=2.若动点E、F同时从点O出发,E点沿折线OA→AD→DC运动,到达C点时停止;F点沿OC运动,到达C点时停止,它们运动的速度都是每秒1个单位长度.设E运动x秒时,△EOF的面积为y(平方单位),则y关于x的函数图象大致为( )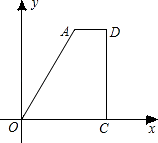
A.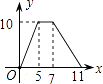
B.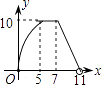
C.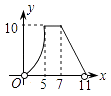
D.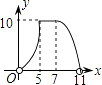
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,垂足分别为E、F.
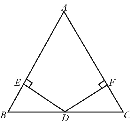
(1)求证;DE=DF;
(2)若∠A=90°,图中与DE相等的还有哪些线段?(不用说明理由)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线AB与CD相交于点O,OF,OD分别是∠AOE,∠BOE的平分线.
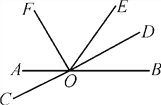
(1)写出∠DOE的补角;
(2)若∠BOE=62°,求∠AOD和∠EOF的度数;
(3)试问射线OD与OF之间有什么特殊的位置关系?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
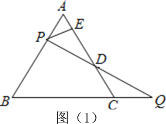
【题目】(1)老师在课上给出了这样一道题目:如图(1),等边△ABC边长为2,过AB边上一点P作PE⊥AC于E,Q为BC延长线上一点,且AP=CQ,连接PQ交AC于D,求DE的长.
小明同学经过认真思考后认为,可以通过过点P作平行线构造等边三角形的方法来解决这个问题.请根据小明同学的思路直接写出DE的长.
(2)(类比探究)
老师引导同学继续研究:
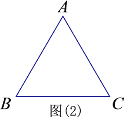
①等边△ABC边长为2,当P为BA的延长线上一点时,作PE⊥CA的延长线于点E ,Q为边BC上一点,且AP=CQ,连接PQ交AC于D.请你在图(2)中补全图形并求DE的长.
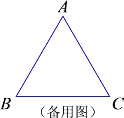
②已知等边△ABC,当P为AB的延长线上一点时,作PE⊥射线AC于点E, Q为哪一个(①BC边上;②BC的延长线上;③CB的延长线上)一点,且AP=CQ,连接PQ交直线AC于点D,能使得DE的长度保持不变.( 直接写出答案的编号)
查看答案和解析>>
科目:初中数学 来源: 题型:
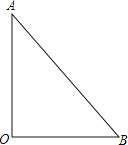
【题目】如图所示,某探险队的A组由驻地O点出发,以12km/h的速度前进,同时,B组也由驻地O出发,以9km/h的速度向另一个方向前进,2h后同时停下来,这时A,B两组相距30km.
(1)此时,A,B两组行进的方向成直角吗?请说明理由;
(2)若A,B两组仍以原速前进,相向而行,经过几小时后相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com