
【题目】初二年级教师对试卷讲评课中学生参与情况进行调查,调查项目分为主动质疑、独立思考、专注听讲、讲解题目四项.调查组随机抽取了若干名初中学生的参与情况,绘制了如图所示的扇形统计图和条形统计图(均不完整),请根据图中所给信息解答下列问题:

(1)在扇形统计图中,项目“主动质疑”所在的扇形的圆心角的度数为______度;
(2)请将频数分布直方图补充完整;
(3)如果全市有6000名初三学生,那么在试卷评讲课中,“独立思考”的初二学生约有多少人?
【答案】(1) 54;(2)补全频数分布直方图见解析;(3)在试卷评讲课中,“独立思考”的初二学生约有1800人.
【解析】
(1)根据专注听讲的人数是224人,所占的比例是40%,即可求得抽查的总人数,继而用360°乘以“主动质疑”的人数所占比例可得答案;
(2)利用总人数减去其他各组的人数,即可求得讲解题目的人数,从而作出频数分布直方图;
(3)利用6000乘以对应的比例即可.
(1)调查的总人数为224÷40%=560(人),∴项目“主动质疑”所在的扇形的圆心角的度数为360°![]() 54°.
54°.
故答案为:54;
(2)选择“讲解题目”的人数为560﹣84﹣168﹣224=84(人),补全频数分布直方图如下:

(3)![]() 6000=1800(人).
6000=1800(人).
答:在试卷评讲课中,“独立思考”的初二学生约有1800人.


科目:初中数学 来源: 题型:
【题目】观察下面一列有序数对:(1,1),(1,2),(2,1),(1,3),(2,2),(3,1),(1,4),(2,3),(3,2),(4,1),(1,5),(2,4),…,按这些规律,第50个有序数对是( )
A. (3,8)B. (4,7)C. (5,6)D. (6,5)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料后解决问题:
小明遇到下面一个问题:
计算(2+1)(22+1)(24+1)(28+1).
经过观察,小明发现如果将原式进行适当的变形后可以出现特殊的结构,进而可以应用平方差公式解决问题,具体解法如下:(2+1)(22+1)(24+1)(28+1)
=(2+1)(2﹣1)(22+1)(24+1)(28+1)
=(22﹣1)(22+1)(24+1)(28+1)
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)
=216﹣1
请你根据小明解决问题的方法,试着解决以下的问题:
(1)(2+1)(22+1)(24+1)(28+1)(216+1)=_____.
(2)(3+1)(32+1)(34+1)(38+1)(316+1)=_____.
(3)化简:(m+n)(m2+n2)(m4+n4)(m8+n8)(m16+n16).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小聪以灵感.他惊喜的发现:当两个全等的直角三角形如图1或图2摆放时,都可以用“面积法”来证明.下面是小聪利用图1证明勾股定理的过程:
(1)将两个全等的直角三角形按图1所示摆放,其中∠DAB=90°.求证:a2+b2=c2.
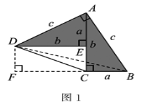
(2)请参照上述证法,利用图2完成下面的证明.
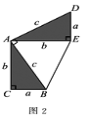
将两个全等的直角三角形按图2所示摆放,其中∠DAB=90°.
求证:a2+b2=c2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一块直角三角板![]() 放置在锐角
放置在锐角![]() 上,使得该三角板的两条直角边
上,使得该三角板的两条直角边![]() 恰好分别经过点
恰好分别经过点![]()
(1)如图①,若![]() 时,点
时,点![]() 在
在![]() 内,则
内,则![]() 度,
度,![]() ____度,
____度,![]() 度;
度;
(2)如图②,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 内,请探究
内,请探究![]() 与
与![]() 之间存在怎样的数量关系,并验证你的结论;
之间存在怎样的数量关系,并验证你的结论;
(3)如图③,改变直角三角板![]() 的位置,使点
的位置,使点![]() 在
在![]() 外,且在
外,且在![]() 边的左侧,直接写出
边的左侧,直接写出![]() 三者之间存在的数量关系.
三者之间存在的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B,C,D在同一条直线上,点E,F分别在直线AD的两侧,且AE=DF,∠A=∠D,AB=DC. 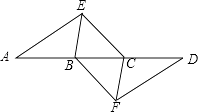
(1)求证:四边形BFCE是平行四边形;
(2)若AD=10,DC=3,∠EBD=60°,则BE=时,四边形BFCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的10张卡片上分别写有11至20十个数字,将它们背面朝上洗匀后,任意抽一张,将下列事件发生的机会的大小填在横线上.
![]()
(1)P1(抽到数字11)=_______;
(2)P2(抽到两位数)=_______,P3(抽到一位数)=_______;
(3)P4(抽到的数大于10)=_______,P5(抽到的数大于16)=_______,P6(抽到的数小于16)=_______;
(4)P7(抽到的数是2的倍数)=_______,P8(抽到的数是3的倍数)=_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC=60°,∠C=45°,AD是BC边上的高,∠ABC的平分线BE交AD于点F,则图中共有等腰三角形( )
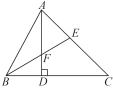
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
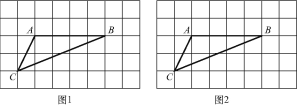
【题目】如图,在8×5的正方形网格中,每个小正方形的边长均为1,△ABC的三个顶点均在小正方形的顶点上.
(1)在图1中画△ABD(点D在小正方形的顶点上),使△ABD的周长等于△ABC的周长,且以A,B,C,D为顶点的四边形是轴对称图形;
(2)在图2中画△ABE(点E在小正方形的顶点上),使△ABE的周长等于△ABC的周长,且以A,B,C,E为顶点的四边形是中心对称图形,并直接写出该四边形的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com