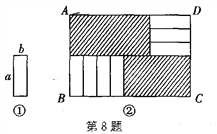
【题目】将7张如图①所示的长为a、宽为b（a>b）的小长方形纸片，按如图②所示的方式不重叠地放在长方形ABCD内，未被覆盖的部分（两个长方形）用阴影表示，设左上角与右下角的阴影部分的面积之差为S，当BC的长度变化时，按照同样的放置方式，S始终保持不变，则a、b应满足( )
A. a＝
b B. a＝3b C. a＝
b D. a＝4b
科目：初中数学 来源： 题型：
【题目】如图，直线l外有不重合的两点A、B．在直线l上求一点C，使得
的长度最短，作法为：①作点B关于直线l的对称点B＇．②连接AB＇交直线l于点C，则点C即为所求．在解决这个问题时，没有用到的知识点是( )
A. 线段的垂直平分线性质 B. 两点之间线段最短
C. 三角形两边之和大于第三边 D. 角平分线的性质
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知:用2辆A型车和1辆B型车载满货物一次可运货11吨；用1辆A型车和2辆B型车载满货物一次可运货13吨.根据以上信息, 解答下列问题：
(1)1辆A型车和l辆B型车都载满货物一次可分别运货多少吨?
(2)某物流公司现有31吨货物，计划同时租用A型车
辆，B型车
辆，一次运完，且恰好每辆车都载满货物请用含有
的式子表示
，并帮该物流公司设计租车方案;
(3)在(2)的条件下，若A型车每辆需租金500元/次，B型车每辆需租金600元/次.请选出最省钱的租车方案，并求出最少租车费用.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知抛物线的顶点为（1，-4），且经过点B（3，0）.
（Ⅰ）求该抛物线的解析式及抛物线与x轴的另一个交点A的坐标；
（Ⅱ）点P(m,t)为抛物线上的一个动点，点P关于原点的对称点为P′.
①当点P′落在该抛物线上时，求m的值；
②当点P′落在第二象限内，P′A2取得最大值时，求m的值.
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】在△ABC中，若∠A=50°，∠B=55°，则△ABC是____________三角形；若∠A=50°，∠B=25°，则△ABC是____________三角形．（填“锐角”，“直角”或“钝角”）
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】对于平面直角坐标系 
中的点
，给出如下定义：记点
到
轴的距离为
，到
轴的距离为
若
≤
，则称
为点
的“引力值”；若
，则称
为点
的“引力值”.特别地，若点
在坐标轴上，则点
的“引力值”为0.
例如，点P（-2,3)到
轴的距离为3 ，到
轴的距离为2 ，因为2<3，所以点
的“引力值”为2.
(1)①点
的“引力值”为 ；②若点
的“引力值”为2，则
的值为 ；
(2)若点C在直线
上，且点C的：“引力值”为2，求点C的坐标；
(3)已知点M是以D（3,4）为圆心，半径为2的圆上的一个动点，那么点M的“引力值”
的取值范围是
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】一根长竹签切成四段，分别为3cm、5cm、7cm、9cm.从中任意选取三根首尾依次相接围成不同的三角形,则围成的三角形共有（ ）
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目：初中数学 来源： 题型：
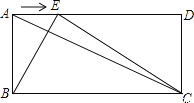
【题目】（14分）如图，已知在矩形ABCD中，AB=a，BC=b，点E是线段AD边上的任意一点（不含端点A、D），连结BE、CE．
（1）若a=5，AC=13，求b．
（2）若a=5，b=10,当BE⊥AC时，求出此时AE的长．
（3）设AE=x，试探索点E在线段AD上运动过程中，使得△ABE与△BCE相似时，求a、b应满足什么条件，并求出此时x的值．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
