
【题目】已知抛物线的顶点为(1,-4),且经过点B(3,0).
(Ⅰ)求该抛物线的解析式及抛物线与x轴的另一个交点A的坐标;
(Ⅱ)点P(m,t)为抛物线上的一个动点,点P关于原点的对称点为P′.
①当点P′落在该抛物线上时,求m的值;
②当点P′落在第二象限内,P′A2取得最大值时,求m的值.
【答案】(Ⅰ)y=x2-2x-3,点A的坐标为(-1,0);(Ⅱ)①m1=![]() ,m2=-
,m2=-![]() . ② m=1.
. ② m=1.
【解析】试题分析: ![]() 由顶点坐标可以设抛物线的解析式为:
由顶点坐标可以设抛物线的解析式为: ![]() 把点
把点![]() 的坐标代入即可求出抛物线的解析式,进而求得抛物线与
的坐标代入即可求出抛物线的解析式,进而求得抛物线与![]() 轴的交点坐标.
轴的交点坐标.
(2)①由对称可表示出![]() 点的坐标,再由
点的坐标,再由![]() 和
和![]() 都在抛物线上,可得到关于
都在抛物线上,可得到关于![]() 的方程,可求得
的方程,可求得![]() 的值;
的值;
②由点![]() 在第二象限,可求得
在第二象限,可求得![]() 的取值范围,利用两点间距离公式可用
的取值范围,利用两点间距离公式可用![]() 表示出
表示出![]() ,再由点
,再由点![]() 在抛物线上,可用消去
在抛物线上,可用消去![]() ,整理可得到关于
,整理可得到关于![]() 的二次函数,利用二次函数的性质可求得其取得最大值时
的二次函数,利用二次函数的性质可求得其取得最大值时![]() 的值,则可求得
的值,则可求得![]() 的值.
的值.
试题解析: ![]() 设抛物线的解析式为
设抛物线的解析式为![]() 代入点
代入点![]() ,
,
![]()
![]()
∴抛物线的解析式为: ![]()
![]()
![]()
∴点![]() 的坐标为
的坐标为![]()
(Ⅱ)①由P(m,t)在抛物线上可得t=m22m3,
∵点P′与P关于原点对称,
∴P′(m,t),
∵点P′落在抛物线上,
![]() 即
即![]()
![]() 解得
解得![]() 或
或![]()
②②由题意可知P′(m,t)在第二象限,
∴m<0,t>0,即m>0,t<0,
∵抛物线的顶点坐标为(1,4),
∴4t<0,
∵P在抛物线上,
![]()
![]()
∵A(1,0),P′(m,t),
![]()
当![]() 时,
时, ![]() 取得最大值.
取得最大值.
把![]() 代入
代入![]() ,得
,得![]()
解得![]()
![]()


科目:初中数学 来源: 题型:
【题目】如图①,CA=CB,CD=CE,∠ACB=∠DCE=α,AD,BE相交于点M,连接CM.
(1)求证:BE=AD;
(2)用含α的式子表示∠AMB的度数;
(3)当α=90°时,取AD,BE的中点分别为点P,Q,连接CP,CQ,PQ,如图②,判断△CPQ的形状,并加以证明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列事件:
①在足球赛中,弱队战胜强队.
②抛掷1枚硬币,硬币落地时正面朝上.
③任取两个正整数,其和大于1
④长为3cm,5cm,9cm的三条线段能围成一个三角形.
其中确定事件有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=60°,∠ABC、∠ACB的平分线交于E,D是AE延长线上一点,且∠BDC=120°.下列结论:①∠BEC=120°;②DB=DC;③DB=DE;④∠BDE=∠BCA.其中正确结论的个数为( )

A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在直线l上依次摆放着七个正方形,已知斜放置的三个正方形的面积分别为1、2、3,正放置的四个正方形的面积依次是S1、S2、S3、S4,则S1+2S2+2S3+S4=________.

查看答案和解析>>
科目:初中数学 来源: 题型:
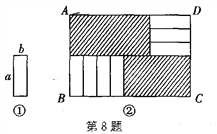
【题目】将7张如图①所示的长为a、宽为b(a>b)的小长方形纸片,按如图②所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b应满足( )
A. a=![]() b B. a=3b C. a=
b B. a=3b C. a=![]() b D. a=4b
b D. a=4b
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学在“助残日”举行了一次“手拉手、献爱心”的捐款活动,学校对已捐款学生人数及捐款金额情况进行了调查.图①表示的是各年级捐款人数占总捐款人数的百分比;图②是学校对学生的捐款金额情况进行抽样调查并根据所得数据绘制的统计图

(1)学校对多少名学生的捐款金额情况进行了抽样调查?
(2)这组捐款金额数据的平均数、中位数各是多少?
(3)若该校九年级共有400名学生捐款,估计全校学生捐款总金额大约多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com