
����Ŀ������ij���ֳ�������ڼ��Ƴ�ѧ��������Ʊ�Żݻ��������Ʊ�۸����±���

ij���Ƶ�λ�������������͵���Ʊ��100�Ž���Ʒѧ���ŵ�����ѧ�����蹺��A��Ʊx�ţ�B��Ʊ������A��Ʊ��3������7�ţ�C��Ʊy�ţ�����������Ϣ����������⣺
��1��ֱ��д��x��y֮��ĺ�����ϵʽ��
��2���蹺Ʊ�ܷ���ΪWԪ����W��Ԫ����x���ţ�֮��ĺ�����ϵʽ��
��3��Ϊ����ѧ�����棬�ƻ�����ѧ����ҹ��Ʊ������20�ţ��ҽڼ���ͨƱ���ٹ���5�ţ����ļ��ֹ�Ʊ���������ַ����������٣�
���𰸡���1��y=93��4x����2��w=��160x+14790����3����A��ƱΪ22�ţ�B��Ʊ73�ţ�C��ƱΪ5��ʱ�������٣����ٷ���Ϊ11270Ԫ��
��������
�����������1��������Ʊ��Ϊ100�õ�x+3x+7+y=100��Ȼ����x��ʾy���ɣ�
��2�����ñ������ݰ�����Ʊ�ķ��ü������õ�w=80x+120��3x+7��+150��93��4x����Ȼ���������ɣ�
��3����������õ�����ʽ�飬�ٽⲻ��ʽ����ȷ������ʽ���������Ϊ20��21��22�����ǵõ�����3�ֹ�Ʊ������Ȼ�����һ�κ�����������w����Сֵ��
�⣺��1���������⣬
x+3x+7+y=100��
����y=93��4x��
��2��w=80x+120��3x+7��+150��93��4x��=��160x+14790��
��3���������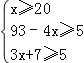
���20��x��22��
��Ϊ����xΪ20��21��22��
���Թ���3�ֹ�Ʊ������A��20��B��67��C��13��A��21��B��70��C��9��A��22��B��73��C��5����
��w=��160x+14790��
��Ϊk=��160��0��
����y��x�����������
���Ե�x=22ʱ��y��С=22������160��+14790=11270��
����A��ƱΪ22�ţ�B��Ʊ73�ţ�C��ƱΪ5��ʱ�������٣����ٷ���Ϊ11270Ԫ��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ��ҩƷ�ڽ����ϼӼ�100%��Ϊԭ�ۣ������ν��ۺ�������Ϊ28%����ƽ��ÿ�εĽ����ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��ڼ������г���ÿ��mԪ�ļ۸����40����Ҷ�������������г���ÿ��nԪ��m��n���ļ۸����ͬ����60����Ҷ������̼���ÿ��![]() Ԫ�ļ۸��������ֲ�Ҷ�����������̵꣨ ��
Ԫ�ļ۸��������ֲ�Ҷ�����������̵꣨ ��
A.ӯ����
B.������
C.��Ӯ����
D.ӯ������ȷ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������y=��x2+2x+m��
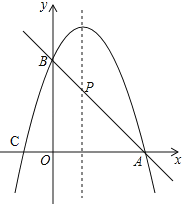
��1����������߹���A��3��0������y�ύ�ڵ�B���������ߵĽ���ʽ����B��C�����ꣻ
��2����ͼ��ֱ��AB�����������ߵĶԳ��ύ�ڵ�P����ֱ��AB�ı���ʽ�͵�P�����꣮
��3������������һ��D��x��y����ʹ��S��ABC=S��ACD�����D�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
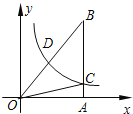
����Ŀ����ͼ����֪˫����y=![]() ��k��0������ֱ��������OABб��OB���е�D����ֱ�DZ�AB�ཻ�ڵ�C������OBC�����Ϊ3����k= ��
��k��0������ֱ��������OABб��OB���е�D����ֱ�DZ�AB�ཻ�ڵ�C������OBC�����Ϊ3����k= ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABC�У�AB=5��AC=6��BC=7����D��E�ֱ���AB��AC�ϣ�DE��BC��
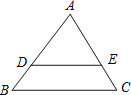
��1����AD��DB=4��3ʱ����DE����
��2������ADE���ܳ����ı���BCED���ܳ���ȣ���DE�ij���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com