
【题目】已知抛物线y=﹣x2+2x+m.
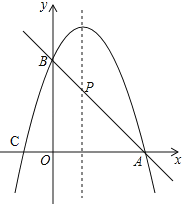
(1)如果抛物线过点A(3,0),与y轴交于点B,求抛物线的解析式及点B、C的坐标;
(2)如图,直线AB与这条抛物线的对称轴交于点P,求直线AB的表达式和点P的坐标.
(3)该抛物线有一点D(x,y),使得S△ABC=S△ACD,求点D的坐标.
【答案】(1)B(0,3);(2)P(1,2);(3)D的坐标为(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3).
,﹣3).
【解析】
试题分析:(1)代入A点的坐标求得m的值即可求得解析式,分别令x=0和y=0,列出方程,解方程即可求得B、C的坐标;
(2)根据待定系数法求得直线AB的解析式,求得抛物线的对称轴x=1,把x=1代入直线的解析式即可求得P的坐标;
(3)根据面积相等且底边相等的三角形的高也应该相等得出D的纵坐标为±3,代入抛物线的解析式即可求得.
解:(1)∵抛物线过点A(3,0),
∴0=﹣9+6+m,
解得m=3,
∴抛物线的解析式为y=﹣x2+2x+3,
令y=0,则,﹣x2+2x+3=0,
解得x1=3,x2=﹣1,
∴C(﹣1,0),
令x=0,得y=3,
∴B(0,3);
(2)∵A(3,0),B(0,3),
设直线AB的解析式为y=kx+b,
∴![]() ,解得
,解得![]() ,
,
∴直线AB的解析式为y=﹣x+3,
∵抛物线y=﹣x2+2x+3=﹣(x﹣1)2+4,
∴对称轴x=1,
把x=1代入y=﹣x+3得y=2,
∴P(1,2);
(3)根据题意得D的纵坐标为±3,
把y=3代入y=﹣x2+2x+3得,﹣x2+2x+3=3,
解得x=0或2,
把y=﹣3代入y=﹣x2+2x+3得,﹣x2+2x+3=﹣3,
解得x=1![]() ,
,
∴D的坐标为(2,3)或(1﹣![]() ,﹣3)或(1+
,﹣3)或(1+![]() ,﹣3).
,﹣3).


 导学教程高中新课标系列答案
导学教程高中新课标系列答案科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,2)、B(n,﹣4)是一次函数y=kx+b的图象与反比例函数![]() 的图象的两个交点.
的图象的两个交点.
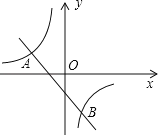
(1)求m、n的值;
(2)求一次函数的关系式;
(3)根据图象写出使一次函数的值小于反比例函数的值的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某游乐场在暑假期间推出学生个人门票优惠活动,各类门票价格如下表:

某慈善单位欲购买三种类型的门票共100张奖励品学兼优的留守学生,设购买A种票x张,B种票张数是A种票的3倍还多7张,C种票y张,根据以上信息解答下列问题:
(1)直接写出x与y之间的函数关系式;
(2)设购票总费用为W元,求W(元)与x(张)之间的函数关系式;
(3)为方便学生游玩,计划购买学生的夜场票不低于20张,且节假日通票至少购买5张,有哪几种购票方案?哪种方案费用最少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com