
如图,O是等边△ABC内一点,OA=3,OB=4,OC=5,将线段BO以点B为旋转中心逆时针旋转60°得到线段BO′,下列结论:
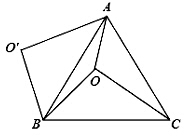
①△BO′A可以由△BOC绕点B逆时针旋转60°得到;
②点O与O′的距离为4;
③∠AOB=150°;
④四边形AO BO′的面积为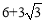 ;
;
⑤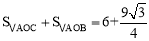 .
.
其中正确的结论是( )
A.①②③ B.①②③④ C.①②③⑤ D.①②③④⑤
科目:初中数学 来源:2016届重庆市江津区三校九年级上学期期中联考数学试卷(解析版) 题型:解答题
操作:如图①,△ABC是等边三角形,△BDC是顶角∠BDC=120°的等腰三角形,以D为顶点作一个60°角:

(1)角的两边分别交AB、AC边于M、N两点,连接MN.探究:线段BM、MN、NC之间的关系,并加以证明.
(2)若角的两边分别交AB、CA的延长线于M、N两点,连接MN。在图②中画出图形,再直接写出线段BM、MN、NC之间的关系.
查看答案和解析>>
科目:初中数学 来源:2015-2016学年重庆市江津区三校八年级上学期期中联考数学试卷(解析版) 题型:解答题
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.试猜想BD,CE,DE三者的数量关系?(直接写出结果)
(2) 如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=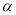 ,其中
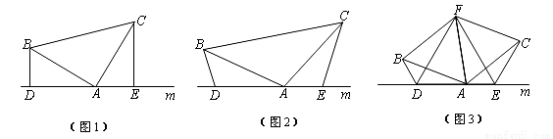
,其中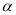 为任意锐角或钝角.请问(1)中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
为任意锐角或钝角.请问(1)中的结论是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3) 拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD、CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源:2015-2016学年重庆市江津区三校八年级上学期期中联考数学试卷(解析版) 题型:选择题
如果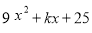 是一个完全平方式,那么k的值是( )
是一个完全平方式,那么k的值是( )
A、30 B、±30 C、15 D、±15
查看答案和解析>>
科目:初中数学 来源:2015-2016学年浙江省八年级上学期第三次月考数学试卷(解析版) 题型:解答题
如图,在△ABC中,∠C=60°,∠A=40°.
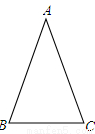
(1)用尺规作图作AB的垂直平分线,交AC于点D,交AB于点E(保留作图痕迹,不要求写作法和证明);
(2)求证:BD平分∠CBA.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com