
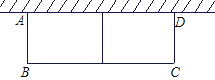
����Ŀ����ͼ��ʾ��ijũ���뽨��һ���ԣ�������ֲ���ֲ�ͬ�Ļ��ܣ��Թ�Ӧ�����г���Ҫ�����ó�Ϊ36m����ʣ�һ����ǽ��ǽ������ʹ�ó���l=13m����Χ���м����һ����ʵij����λ��ԣ��軨�Կ�ABΪx�����ΪS��
��1����S��x�ĺ�����ϵʽ����ָ������һ�κ��������Ƕ��κ�����
��2����ҪΧ�����Ϊ96m2�Ļ��ԣ����AB�ij��ȣ�
��3�����Ե�����ܴﵽ108m2�����ܣ������AB�ij��ȣ���������˵�����ɣ�
���𰸡���1��S=��36-3x��x=-3x2+36x��
��2��AB�ij�Ϊ8m��
��3�����Ե�������ܴﵽ108m2��
�������������������1��������ϵΪ������ʳ�-3AB����AB=S�����ɵó��𰸣�
��2��������ϵΪ������ʳ�-3AB����AB=96���������ֵ������ú��ʵĽ⼴�ɣ�
��3���ѣ�1�����ô���ʽ��ʾ���������Ϊa��x-h��2+b����ʽ�ɵ����������
�������������1���軨�Կ�ABΪx�����ΪS��
��S=��36-3x��x=-3x2+36x��
��2����AB�ij���x�ף�
��36-3x��x=96��
���x1=4��x2=8��
��x=4ʱ�������λ��Եij�Ϊ36-3x=24����ǽ�������ó���a��13m������ȥ��
��x=8ʱ�������λ��Եij�Ϊ24-3x=12���������⣻
��AB�ij�Ϊ8m��
��3�����Ե����ΪS=��36-3x��x=-3��x-6��2+108��
�൱AB��Ϊ6m����Ϊ16mʱ������������Ϊ108ƽ���ף�
�֡ߵ�AB=6mʱ�������λ��Եij�Ϊ36-3��6=18m����ǽ�������ó���a��13m������ȥ��
�ʻ��Ե�������ܴﵽ108m2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�� ��֪����ͼ�߳�Ϊ2��������ABCD�У���MAN�����߷ֱ�BC��CD����M��N���㣬 �ҡ�MAN=45.

��1����֤��MN=BM+DN.
��2����AM��AN���Խ���BD��E��F���㣬��BF=y��DE=x,��y��x�ĺ�����ϵʽ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������ʽ��a��1��x��a��1�Ľ���x��1����a��ȡֵ��Χ�ǣ�������
A. a��1B. a��1C. a��1D. a��1
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����һƪ�����У����ġ����ء����͡������ֹ�����100�Σ���֪���ġ��͡��ء���Ƶ��֮����0.7����ô���͡��ֳ��ֵ�Ƶ����(����)
A. 28 B. 30 C. 32 D. 34
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͬһ����ϵ����һ�κ���y=ax+b����κ���y=ax2��b��ͼ������ǣ� ��
A. 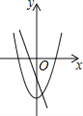 B.
B. 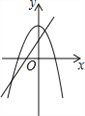 C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�Ծ�����20����,ÿ����ѡ�Ե�10��,ѡ���˻��߲�ѡ��5��,����Ҫѡ��________����,��÷ֲ��ܲ�����80��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��һ����Ȼ�����ܱ�ʾΪ����������Ȼ����ƽ����������Ȼ��Ϊ���ǻ����������磺22-12=3��3�����ǻ�������0��ʼ��������2019���ǻ�������_______ ����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ����Rt��ABC�У���C=90�㣬��BAC�Ľ�ƽ����AD��BC����D��
��1����AB����һ��OΪԲ�ģ���A��D��������O����д������������ͼ�ۼ��������ж�ֱ��BC���O��λ�ù�ϵ����˵�����ɣ�
��2������1���еġ�O��AB�ߵ���һ������ΪE��AB=6��BD=2![]() �����߶�BD��BE���ӻ�DE��Χ�ɵ�ͼ�������������������źͦУ�
�����߶�BD��BE���ӻ�DE��Χ�ɵ�ͼ�������������������źͦУ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com