
科目:初中数学 来源: 题型:选择题
| A. | 甲班 | B. | 乙班 | C. | 两班一样整齐 | D. | 无法确定 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
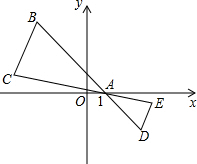 如图,在△ABC中,B,C两个顶点在x轴的上方,点A的坐标是(1,0),以点A为位似图形,并把△ABC的边长缩小为原来的$\frac{1}{2}$倍,记所得的位似图形为△ADE.设点C的对应点E的横坐标为a,则点C的横坐标为( )
如图,在△ABC中,B,C两个顶点在x轴的上方,点A的坐标是(1,0),以点A为位似图形,并把△ABC的边长缩小为原来的$\frac{1}{2}$倍,记所得的位似图形为△ADE.设点C的对应点E的横坐标为a,则点C的横坐标为( )| A. | $\frac{1}{2}$(a-1) | B. | $\frac{1}{2}$(a+1) | C. | 3-2a | D. | 2(a-1) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,为测量某建筑物BC及上面旗杆AB的高度,小明在距建筑物BC底部12m的点F处,测得视线点E与旗杆AB的顶端A的仰角为52°,测得视线点E与旗杆AB的底端B是仰角为45°,已知小明的身高EF为1.6m.
如图,为测量某建筑物BC及上面旗杆AB的高度,小明在距建筑物BC底部12m的点F处,测得视线点E与旗杆AB的顶端A的仰角为52°,测得视线点E与旗杆AB的底端B是仰角为45°,已知小明的身高EF为1.6m.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
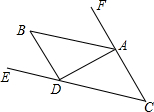 如图,已知AB∥CD,AB是∠FAD的平分线,∠C=45°.
如图,已知AB∥CD,AB是∠FAD的平分线,∠C=45°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com