
 如图,为测量某建筑物BC及上面旗杆AB的高度,小明在距建筑物BC底部12m的点F处,测得视线点E与旗杆AB的顶端A的仰角为52°,测得视线点E与旗杆AB的底端B是仰角为45°,已知小明的身高EF为1.6m.
如图,为测量某建筑物BC及上面旗杆AB的高度,小明在距建筑物BC底部12m的点F处,测得视线点E与旗杆AB的顶端A的仰角为52°,测得视线点E与旗杆AB的底端B是仰角为45°,已知小明的身高EF为1.6m.分析 (1)先过点E作ED⊥BC于D,由视线点E与旗杆AB的底端B的仰角为45°得BD=ED=FC=12,DC=EF=1.6,从而求出BC;
(2)由已知由视线点E与旗杆AB的顶端A的仰角52°可求出AD,则AB=AD-BD.
解答 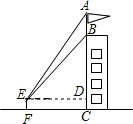 解:(1)过点E作ED⊥AC于点D,则四边形DCFE为矩形.
解:(1)过点E作ED⊥AC于点D,则四边形DCFE为矩形.
∴∠ADE=90°,CD=EF=1.6,ED=FC=12.
在Rt△BED中,∵DE=12,∠BED=45°,
∴BD=ED•tan∠BED=12×tan45°=12.
∴BC=BD+CD=12+1.6=13.6(m).
答:建筑物BC的高度为13.6m;
(2)在Rt△AED中,∵DE=12,∠AED=52°,
∴AD=ED•tan∠AED=12×tan52°=15.36.
∴AB=AD-BD=15.36-12=3.36≈3.4(m).
答:旗杆AB的高度约为3.4m.
点评 此题考查的知识点是解直角三角形的应用,解题的关键是把实际问题转化为解直角三角形问题,先得到等腰直角三角形,再根据三角函数求解.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:解答题
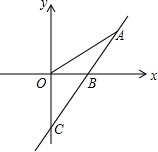 如图,直线y=kx-4与x轴,y轴分别交于B、C两点.且tan∠OBC=$\frac{4}{3}$.
如图,直线y=kx-4与x轴,y轴分别交于B、C两点.且tan∠OBC=$\frac{4}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:
如图,在平面直角坐标系中,点P(m,n)是动点,且m、n的关系满足下表:| m | … | -3 | -2 | 0 | 1 | 2 | 3 | … |
| n | … | 4 | 3 | 1 | 0 | -1 | -2 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
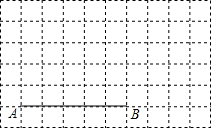 如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.
如图,在10×6的正方形网络中,每一个小正方形的边长均为1,线段AB的端点A、B均为在小正方形的顶点上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com