
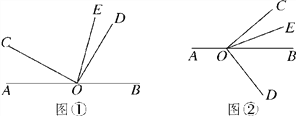
【题目】已知O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
(1)如图①,若∠AOC=30°,求∠DOE的度数;
(2)在图①中,若∠AOC=![]() ,直接写出∠DOE的度数(用含
,直接写出∠DOE的度数(用含![]() 的代数式表示);
的代数式表示);
(3)将图①中的∠DOC绕顶点O顺时针旋转至图②的位置,探究∠AOC和∠DOE的度数之间的关系,写出你的结论,并说明理由;
【答案】见解析
【解析】试题分析:(1)由已知可求出∠BOC=180°-∠AOC=150°,再由∠COD是直角,OE平分∠BOC求出∠DOE的度数;
(2)由(1)可得出结论∠DOE=![]() ∠AOC,从而用含a的代数式表示出∠DOE的度数;
∠AOC,从而用含a的代数式表示出∠DOE的度数;
(3)①由∠COD是直角,OE平分∠BOC可得出∠COE=∠BOE=90°-∠DOE,则得∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),从而得出∠AOC和∠DOE的度数之间的关系.
试题解析:(1)由已知得∠BOC=180°-∠AOC=150°,
又∠COD是直角,OE平分∠BOC,
∴∠DOE=∠COD-![]() ∠BOC=90°-
∠BOC=90°-![]() ×150°=15°.
×150°=15°.
(2)∠DOE=![]()
![]() .
.
由(1)知∠DOE=∠COD-![]() ∠BOC=90°,
∠BOC=90°,
∴∠DOE=90°-![]() (180°-∠AOC)=
(180°-∠AOC)= ![]() ∠AOC=
∠AOC=![]()
![]() .
.
(3)∠AOC=2∠DOE. 理由如下:
∵∠COD是直角,OE平分∠BOC,∴∠COE=∠BOE=90°-∠DOE,
∴∠AOC=180°-∠BOC=180°-2∠COE=180°-2(90°-∠DOE),
∴∠AOC=2∠DOE.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:初中数学 来源: 题型:
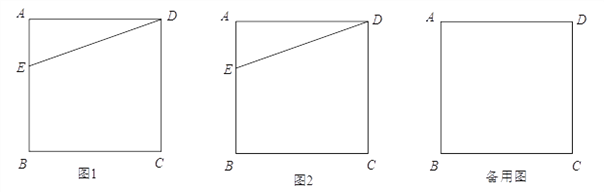
【题目】如图,在正方形ABCD中,E为AB边上一点,连接DE,将△ADE绕点D逆时针旋转90°得到△CDF,作点F关于CD的对称点,记为点G,连接DG.
(1)依题意在图1中补全图形;
(2)连接BD,EG,判断BD与EG的位置关系并在图2中加以证明;
(3)当点E为线段AB的中点时,直接写出∠EDG的正切值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景区在“五一”小长假期间,每天接待的旅客人数统计如下表.
日期 | 5月1日 | 5月2日 | 5月3日 | 5月4日 | 5月5日 |
人数(万人) | 1.2 | 2 | 2.5 | 2 | 1.1 |
表中表示人数的一组数据中,众数和中位数分别为( )
A.2.5万,2万B.2.5万,2.5万C.2万,2.5万D.2万,2万
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八(1)班开展男生、女生垫排球比赛活动,每队各派5名同学参加.死皮赖脸是男生队和女生队5名同学的比赛数据(单位:个):
1号 | 2号 | 3号 | 4号 | 5号 | |
男生队 | 100 | 98 | 110 | 89 | 103 |
女生队 | 88 | 100 | 95 | 120 | 97 |
请回答下列问题:
(1)计算两队的平均成绩;
(2)从成绩稳定性角度考虑,哪队成绩稍好,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC内部取一点P,使得点P到△ABC的三边的距离相等,则点P应是△ABC的下列哪三条线段的交点( )
A. 高 B. 中线 C. 垂直平分线 D. 角平分线
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com