
【题目】已知抛物线![]() ,其中
,其中![]() 是常数,该抛物线的对称轴为直线
是常数,该抛物线的对称轴为直线![]() .
.
(![]() )求该抛物线的函数解析式.
)求该抛物线的函数解析式.
(![]() )把该抛物线沿
)把该抛物线沿![]() 轴向上平移多少个单位后,得到的抛物线与
轴向上平移多少个单位后,得到的抛物线与![]() 轴只有一个公共点.
轴只有一个公共点.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:
(1)把抛物线的解析式整理为一般形式,由此可得到其对称轴的表达式,结合对称轴是直线![]() 即可解出“m”的值,从而可求得其解析式;
即可解出“m”的值,从而可求得其解析式;
(2)设把该抛物线向上平移![]() 个单位长度后与
个单位长度后与![]() 轴只有一个公共点,由此可得新的解析式的表达式,再由“△=
轴只有一个公共点,由此可得新的解析式的表达式,再由“△=![]() ”即可求得
”即可求得![]() 的值.
的值.
试题解析:
(1)∵![]() 可化为:
可化为: ![]() ,
,
∴该抛物线的对称轴为直线: ![]() ,
,
又∵该抛物线的对称轴为:直线![]() ,
,
∴![]() ,解得:
,解得: ![]() ,
,
∴抛物线的解析式为: ![]() ;
;
(![]() )设原抛物线向上平移
)设原抛物线向上平移![]() 个单位后与
个单位后与![]() 轴只有1个公共点,则平移后抛物线解析式为:
轴只有1个公共点,则平移后抛物线解析式为:
![]() ,
,
∵它与![]() 轴只有一个公共点,
轴只有一个公共点,
∴![]() ,解得:
,解得: ![]() ,
,
即,将该抛物线向上平移![]() 个单位长度后,新抛物线与
个单位长度后,新抛物线与![]() 轴只有1个公共点.
轴只有1个公共点.


科目:初中数学 来源: 题型:
【题目】已知:△ABC为等边三角形
(1)若D为△ABC外一点,满足∠CDB=30,求证:![]()
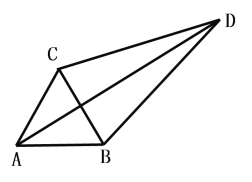
(2)若D为△ABC内一点,DC=3,DB=4,DA=5,求∠CDB的度数
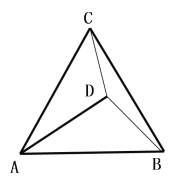
(3)若D为△ABC内一点,DA=4,DB=![]() ,DC=
,DC=![]() 则AB= (直接写出答案)
则AB= (直接写出答案)
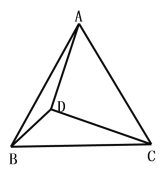
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,△BPC是等边三角形,BP、CP的延长线分别交AD于点E 、F ,连结BD 、DP ,BD与CF相交于点H. 给出下列结论:①△BDE ∽△DPE;② ![]() ;③DP 2=PH ·PB; ④
;③DP 2=PH ·PB; ④![]() . 其中正确的是( ).
. 其中正确的是( ).
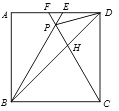
A. ①②③④ B. ①②④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列调查中,调查方式选择最合理的是![]()
![]()
A. 为了解安徽省中学生的课外阅读情况,选择全面调查
B. 调查七年级某班学生打网络游戏的情况,选择抽样调查
C. 为确保长征六号遥二火箭成功发射,应对零部件进行全面调查
D. 为了解一批袋装食品是否含有防腐剂,选择全面调查
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:

操作一:如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE.
(1)如果AC=6cm,BC=8cm,可求得△ACD的周长为 ;
(2)如果∠CAD:∠BAD=4:7,可求得∠B的度数为 ;
操作二:如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=9cm,BC=12cm,请求出CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),公路上有A、B、C三个车站,一辆汽车从A站以速度v1匀速驶向B站,到达B站后不停留,以速度v2匀速驶向C站,汽车行驶路程y(千米)与行驶时间x(小时)之间的函数图象如图(2)所示.

(1)当汽车在A、B两站之间匀速行驶时,求y与x之间的函数关系式及自变量的取值范围;
(2)求出v2的值;
(3)若汽车在某一段路程内刚好用50分钟行驶了90千米,求这段路程开始时x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数![]() ,
, ![]() .在同一平面直线坐标系中
.在同一平面直线坐标系中
(![]() )若函数
)若函数![]() 的图象过点
的图象过点![]() ,函数
,函数![]() 的图象过点
的图象过点![]() ,求
,求![]() ,
, ![]() 的值.
的值.
(![]() )若函数
)若函数![]() 的图象经过
的图象经过![]() 的顶点.
的顶点.
①求证: ![]() .
.
②当![]() 时,比较
时,比较![]() ,
, ![]() 的大小.
的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
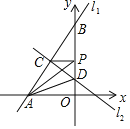
【题目】已知直线![]() :
:![]() 与直线
与直线![]() :
:![]() 都经过
都经过![]() ,直线
,直线![]() 交y轴于点
交y轴于点![]() ,交x轴于点A,直线
,交x轴于点A,直线![]() 交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组
交y轴于点D,P为y轴上任意一点,连接PA、PC,有以下说法:①方程组 的解为
的解为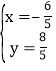 ;②
;②![]() 为直角三角形;③
为直角三角形;③![]() ;④当
;④当![]() 的值最小时,点P的坐标为
的值最小时,点P的坐标为![]() 其中正确的说法个数有
其中正确的说法个数有![]()
![]()
A. 1个B. 2个C. 3个D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请将下列证明过程补充完整:
已知:如图,AE平分∠BAC,CE平分∠ACD,且∠α+∠β=90°.
求证:AB∥CD.
证明:∵CE平分∠ACD (已知),
∴∠ACD=2∠α(______________________)
∵AE平分∠BAC (已知),
∴∠BAC=_________(______________________)
∵∠α+∠β=90°(已知),
∴2∠α+2∠β=180°(等式的性质)
∴∠ACD+∠BAC==_________(______________________)
∴AB∥CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com