
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | p |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)分别求yA,yB关于x的函数关系式;
(2)选择哪种方式上网学习合算,为什么?
【答案】(1)![]() ;
;![]() ;
;
(2) 当0<x<30时,yA<yB,选择A方式上网学习合算,当x=30时,yA=yB,选择哪种方式上网学习都行,当x>30时,yA>yB,选择B方式上网学习合算.理由见解析.
【解析】
(1)根据已知条件即可求得yA与x之间的函数关系式为:当x≤25时,yA=7;当x>25时,yA=7+(x-25)×60×0.01,
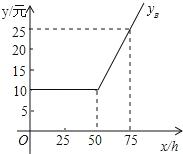
由图象知:m=10,n=50,超时费![]() =0.6(元/h);进而求出yB与x之间函数关系为:当x≤50时,yB=10;当x>50时,yB=10+(x-50)×0.6;
=0.6(元/h);进而求出yB与x之间函数关系为:当x≤50时,yB=10;当x>50时,yB=10+(x-50)×0.6;
(2)分0<x≤25;25<x≤50;x>50三种情况分别讨论即可.
解:(1)由表格可知:
当x≤25时,yA=7;
当x>25时,yA=7+(x﹣25)×60×0.01,yA=0.6x﹣8,
则yA与x之间的函数关系式为:yA=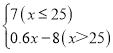 ;
;
由图象知:m=10,n=50,超时费![]() =0.6(元/h);
=0.6(元/h);
当x≤50时,yB=10,
当x>50时,yB=10+(x﹣50)×0.6=0.6x﹣20,
则yB与x之间的函数关系式为:yB=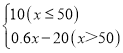 ;
;
(2)①当0<x≤25时,
∵yA=7,yB=50,
∴yA<yB,
∴选择A方式上网学习合算;
②当25<x≤50时,
如果yA=yB,即0.6x﹣8=10,解得x=30,
∴当25<x<30时,yA<yB,选择A方式上网学习合算;
当x=30时,yA=yB,选择哪种方式上网学习都行;
当30<x≤50,yA>yB,选择B方式上网学习合算;
③当x>50时,
∵yA=0.6x﹣8,yB=0.6x﹣20,yA>yB,
∴选择B方式上网学习合算.
综上所述:当0<x<30时,yA<yB,选择A方式上网学习合算,
当x=30时,yA=yB,选择哪种方式上网学习都行,
当x>30时,yA>yB,选择B方式上网学习合算.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
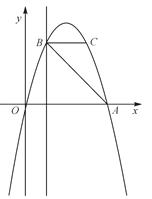
【题目】如图,抛物线y=ax2+bx(a≠0)过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,是否存在这样的点P,使得△ABP的面积为△ABC面积的2倍?若存在,求出点P的坐标,若不存在,请说明理由;
(4)若点M在直线BH上运动,点N在x轴正半轴上运动,当以点C,M,N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=AC,∠A=36°.
(1)用尺规作图作∠ABC的角平分线,交AC于点D;(保留作图痕迹,不写作法).
(2)求证:△BCD是等腰三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
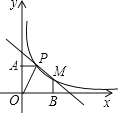
【题目】如图,已知反比例函数![]() 的图象和一次函数
的图象和一次函数![]() 的图象都过点
的图象都过点![]() ,过点P作y轴的垂线,垂足为A,O为坐标原点,
,过点P作y轴的垂线,垂足为A,O为坐标原点,![]() 的面积为1.
的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
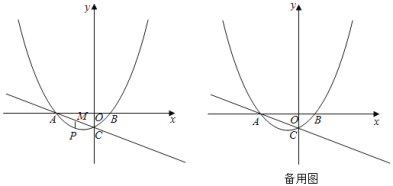
【题目】如图,抛物线![]() 交x轴于A,B两点,交y轴于点C.直线
交x轴于A,B两点,交y轴于点C.直线![]() 经过点A,C.
经过点A,C.
(1)求抛物线的解析式;
(2)点P是抛物线上一动点,过点P作x轴的垂线,交直线AC于点M,设点P的横坐标为m.
①当![]() 是直角三角形时,求点P的坐标;
是直角三角形时,求点P的坐标;
②作点B关于点C的对称点![]() ,则平面内存在直线l,使点M,B,
,则平面内存在直线l,使点M,B,![]() 到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线
到该直线的距离都相等.当点P在y轴右侧的抛物线上,且与点B不重合时,请直接写出直线![]() 的解析式.(k,b可用含m的式子表示)
的解析式.(k,b可用含m的式子表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
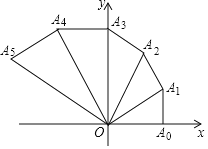
【题目】如图,Rt△OA0A1在平面直角坐标系内,∠OA0A1=90°,∠A0OA1=30°,以OA1为直角边向外作Rt△OA1A2,使∠OA1A2=90°,∠A1OA2=30°,以OA2为直角边向外作Rt△OA2A3,使∠OA2A3=90°,∠A2OA3=30°,按此方法进行下去,得到Rt△OA3A4,Rt△OA4A5,…,Rt△OA2018A2019,若点A0(1,0),则点A2019的横坐标为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场对某种商品进行销售,第x天的销售单价为m元/件,日销售量为n件,其中m,n分别是x(1≤x≤30,且x为整数)的一次函数,销售情况如下表:

(1)过程表中数据,分别直接写出m与x,n与x的函数关系式: , ;
(2)求商场销售该商品第几天时该商品的日销售额恰好为3600元?
(3)销售商品的第15天为儿童节,请问:在儿童节前(不包括儿童节当天)销售该商品第几天时该商品的日销售额最多?商场决定将这天该商品的日销售额捐献给儿童福利院,试求出商场可捐款多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
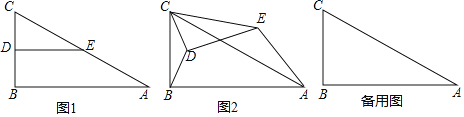
【题目】如图1,在![]() 中,
中,![]() ,点
,点![]() 分别是边
分别是边![]() 的中点,连接
的中点,连接![]() .将
.将![]() 绕点
绕点![]() 逆时针方向旋转,记旋转角为
逆时针方向旋转,记旋转角为![]() .
.
![]() 问题发现
问题发现
![]() 当
当![]() 时,
时,![]() ;
;![]() 当
当![]() 时,
时,![]() .
.
![]() 拓展探究
拓展探究
试判断:当![]() 时,
时,![]() 的大小有无变化?请仅就图2的情形给出证明.
的大小有无变化?请仅就图2的情形给出证明.
![]() 问题解决
问题解决
![]() 绕点
绕点![]() 逆时针旋转至
逆时针旋转至![]() 三点在同一条直线上时,求线段
三点在同一条直线上时,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年中国北京世界园艺博览会(以下简称“世园会”)于4月29日至10月7日在北京延庆区举行.世园会为满足大家的游览需求,倾情打造了4条各具特色的趣玩路线,分别是:![]() .“解密世园会”、
.“解密世园会”、![]() .“爱我家,爱园艺”、
.“爱我家,爱园艺”、![]() .“园艺小清新之旅”和
.“园艺小清新之旅”和![]() .“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
.“快速车览之旅”.李欣和张帆都计划暑假去世园会,他们各自在这4条线路中任意选择一条线路游览,每条线路被选择的可能性相同.
(1)李欣选择线路![]() .“园艺小清新之旅”的概率是多少?
.“园艺小清新之旅”的概率是多少?
(2)用画树状图或列表的方法,求李欣和张帆恰好选择同一线路游览的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com