
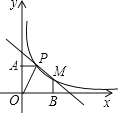
【题目】如图,已知反比例函数![]() 的图象和一次函数
的图象和一次函数![]() 的图象都过点
的图象都过点![]() ,过点P作y轴的垂线,垂足为A,O为坐标原点,
,过点P作y轴的垂线,垂足为A,O为坐标原点,![]() 的面积为1.
的面积为1.
(1)求反比例函数和一次函数的解析式;
(2)设反比例函数图象与一次函数图象的另一交点为M,过M作x轴的垂线,垂足为B,求五边形![]() 的面积.
的面积.
【答案】(1)反比例函数的解析式为![]() ;一次函数的解析式为
;一次函数的解析式为![]() ;(2)
;(2)![]()
【解析】
(1)根据系数k的几何意义即可求得k,进而求得![]() ,然后利用待定系数法即可求得一次函数的解析式;
,然后利用待定系数法即可求得一次函数的解析式;
(2)设直线![]() 交x轴、y轴于C、D两点,求出点C、D的坐标,然后联立方程求得P、M的坐标,最后根据
交x轴、y轴于C、D两点,求出点C、D的坐标,然后联立方程求得P、M的坐标,最后根据![]() ,根据三角形的面积公式列式计算即可得解;
,根据三角形的面积公式列式计算即可得解;
解:(1)∵过点P作y轴的垂线,垂足为A,O为坐标原点,![]() 的面积为1.
的面积为1.
∴![]() ,
,
∴![]() ,
,
∵在第一象限,
∴![]() ,
,
∴反比例函数的解析式为![]() ;
;
∵反比例函数![]() 的图象过点
的图象过点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵次函数![]() 的图象过点
的图象过点![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴一次函数的解析式为![]() ;
;
(2)设直线![]() 交x轴、y轴于C、D两点,
交x轴、y轴于C、D两点,
∴![]() ,
,![]() ,
,
解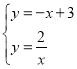 得
得![]() 或
或![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴五边形![]() 的面积为:
的面积为:![]() .
.


 走进文言文系列答案
走进文言文系列答案科目:初中数学 来源: 题型:
【题目】如图表示的是某班部分同学衣服上口袋的数目.
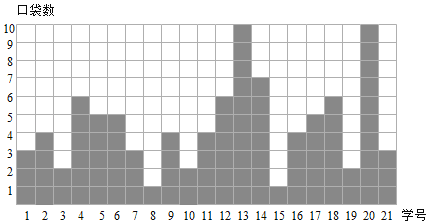
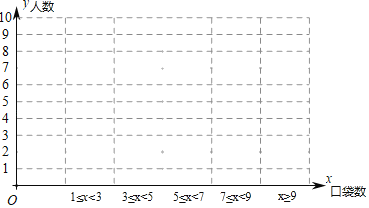
①从图中给出的信息得到学生衣服上口袋数目的中位数为 ,众数为 .
②根据如图信息,在给出的图表中绘制频数条形统计图,由此估计该班学生衣服上口袋数目为![]() 的概率.
的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
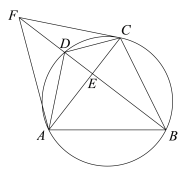
【题目】如图,四边形ABCD内接于⊙O,AB=AC,BD⊥AC,垂足为E,点F在BD的延长线上,且DF=DC,连接AF、CF.
(1)求证:∠BAC=2∠DAC;
(2)若AF=10,BC=4![]() ,求tan∠BAD的值.
,求tan∠BAD的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知直线![]() 与抛物线
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
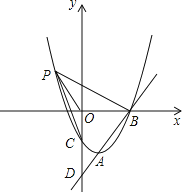
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
查看答案和解析>>
科目:初中数学 来源: 题型:
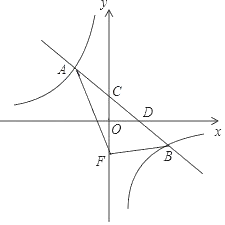
【题目】在平面直角坐标系中,一次函数y=﹣![]() x+b的图象与反比例函数y=
x+b的图象与反比例函数y=![]() (k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(k≠0)图象交于A、B两点,与y轴交于点C,与x轴交于点D,其中A点坐标为(﹣2,3).
(1)求一次函数和反比例函数解析式.
(2)若将点C沿y轴向下平移4个单位长度至点F,连接AF、BF,求△ABF的面积.
(3)根据图象,直接写出不等式﹣![]() x+b>
x+b>![]() 的解集.
的解集.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】模具厂计划生产面积为4,周长为m的矩形模具.对于m的取值范围,小亮已经能用“代数”的方法解决,现在他又尝试从“图形”的角度进行探究,过程如下:
(1)建立函数模型
设矩形相邻两边的长分别为x,y,由矩形的面积为4,得![]() ,即
,即![]() ;由周长为m,得
;由周长为m,得![]() ,即
,即![]() .满足要求的
.满足要求的![]() 应是两个函数图象在第 象限内交点的坐标.
应是两个函数图象在第 象限内交点的坐标.
(2)画出函数图象
函数![]() 的图象如图所示,而函数
的图象如图所示,而函数![]() 的图象可由直线
的图象可由直线![]() 平移得到.请在同一直角坐标系中直接画出直线
平移得到.请在同一直角坐标系中直接画出直线![]() .
.
(3)平移直线![]() ,观察函数图象
,观察函数图象
①当直线平移到与函数![]() 的图象有唯一交点
的图象有唯一交点![]() 时,周长m的值为 ;
时,周长m的值为 ;
②在直线平移过程中,交点个数还有哪些情况?请写出交点个数及对应的周长m的取值范围.
(4)得出结论
若能生产出面积为4的矩形模具,则周长m的取值范围为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
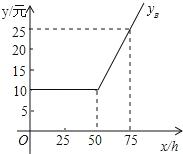
【题目】随着信息技术的快速发展,“互联网+”渗透到我们日常生活的各个领域,网上在线学习交流已不再是梦,现有某教学网站策划了A,B两种上网学习的月收费方式
收费方式 | 月使用费/元 | 包时上网时间/h | 超时费(元/min) |
A | 7 | 25 | 0.01 |
B | m | n | p |
设每月上网学习时间为x小时,方案A,B的收费金额分别为yA,yB.
(1)分别求yA,yB关于x的函数关系式;
(2)选择哪种方式上网学习合算,为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,M,N,P,Q分别为边AB,BC,CD,DA上的点(不与端点重合).
对于任意矩形ABCD,下面四个结论中,①存在无数个四边形MNPQ是平行四边形;②存在无数个四边形MNPQ是矩形;③存在无数个四边形MNPQ是菱形;④至少存在一个四边形MNPQ是正方形.所有正确结论的序号是______.
查看答案和解析>>
科目:初中数学 来源: 题型:
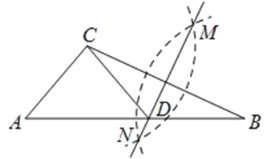
【题目】如图,在已知的![]() 中,按以下步骤作图:①分别以
中,按以下步骤作图:①分别以![]() 为圆心,以大于
为圆心,以大于![]() 的长为半径作弧,两弧相交于两点
的长为半径作弧,两弧相交于两点![]() ;②作直线
;②作直线![]() 交
交![]() 于点
于点![]() ,连接
,连接![]() .若
.若![]() ,
,![]() ,则
,则![]() 的度数为( )
的度数为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com