
【题目】如图,已知直线![]() 与抛物线
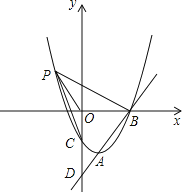
与抛物线![]() 相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
相交于A,B两点,且点A(1,-4)为抛物线的顶点,点B在x轴上。
(1)求抛物线的解析式;
(2)在(1)中抛物线的第二象限图象上是否存在一点P,使△POB与△POC全等?若存在,求出点P的坐标;若不存在,请说明理由;
(3)若点Q是y轴上一点,且△ABQ为直角三角形,求点Q的坐标。
【答案】解:(1)把A(1,-4)代入![]() ,得k=2,∴
,得k=2,∴![]() 。
。
令y=0,解得:x=3,∴B的坐标是(3,0)。
∵A为顶点,∴设抛物线的解析为![]() 。
。
把B(3,0)代入得:4a-4=0,解得a=1。
∴抛物线的解析式为![]() 即
即![]() 。
。
(2)存在。
∵OB=OC=3,OP=OP,∴当∠POB=∠POC时,△POB≌△POC。
此时PO平分第二象限,即PO的解析式为y=-x。
设P(m,-m),则![]() ,解得
,解得![]() (
(![]() ,舍去)。
,舍去)。
∴P(![]() 。
。
(3)①如图,当∠Q1AB=90°时,△DAQ1∽△DOB,

∴![]() ,即
,即![]() 。∴
。∴![]() 。
。
∴![]() ,即
,即![]() 。
。
②如图,当∠Q2BA=90°时,△BOQ2∽△DOB,
∴![]() ,即
,即![]() 。
。
∴![]() ,即
,即![]() 。
。
③如图,当∠AQ3B=90°时,作AE⊥y轴于E,则△BOQ3∽△Q3EA,
∴![]() ,即
,即![]() 。
。
∴![]() ,解得OQ3=1或3,即Q3(0,-1),Q4(0,-3)。
,解得OQ3=1或3,即Q3(0,-1),Q4(0,-3)。
综上,Q点坐标为![]() 或
或![]() 或(0,-1)或(0,-3)。
或(0,-1)或(0,-3)。
【解析】
试题(1)已知点A坐标可确定直线AB的解析式,进一步能求出点B的坐标.点A是抛物线的顶点,那么可以将抛物线的解析式设为顶点式,再代入点B的坐标,依据待定系数法可解。
(2)首先由抛物线的解析式求出点C的坐标,在△POB和△POC中,已知的条件是公共边OP,若OB与OC不相等,那么这两个三角形不能构成全等三角形;若OB等于OC,那么还要满足的条件为:∠POC=∠POB,各自去掉一个直角后容易发现,点P正好在第二象限的角平分线上,联立直线y=-x与抛物线的解析式,直接求交点坐标即可,同时还要注意点P在第二象限的限定条件。
(3)分别以A、B、Q为直角顶点,分类进行讨论,找出相关的相似三角形,依据对应线段成比例进行求解即可。


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】图1所示的是某超市入口的双翼闸门,如图2,当它的双翼展开时,双翼边缘的端点A与B 之间的距离为10cm,双翼的边缘AC=BD=54cm,且与闸机侧立面夹角∠PCA=∠BDQ=30°,求当双翼收起时,可以通过闸机的物体的最大宽度。


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线y=x2+bx+c与x轴交于点A,B,AB=2,与y轴交于点C,对称轴为直线x=2.
(1)求抛物线的函数表达式;
(2)根据图像,直接写出不等式x2+bx+c>0的解集: .
(3)设D为抛物线上一点,E为对称轴上一点,若以点A,B,D,E为顶点的四边形是菱形,则点D的坐标为: .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“农民也能报销医疗费了!”这是国家推行新型农村医疗合作的成果.村民只要每人每年交10元钱,就可以加入合作医疗,每年先由自己支付医疗费,年终时可得到按一定比例返回的返回款,这一举措极大地增强了农民抵御大病风险的能力.小华与同学随机调查了他们乡的一些农民,根据收集到的数据绘制了以下的统计图.
根据以上信息,解答以下问题:
(1)本次调查了 名村民,被调查的村民中,有 人参加合作医疗得到了返回款?
(2)若该乡有10000名村民,请你估计有多少人参加了合作医疗?要使两年后参加合作医疗的人数增加到9680人,假设这两年的年平均增长率相同,求年平均增长率.

查看答案和解析>>
科目:初中数学 来源: 题型:
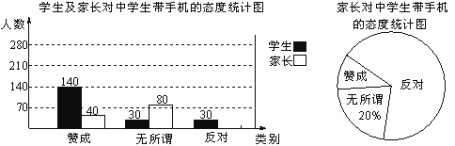
【题目】“校园手机”现象越来越受到社会的关注,小记者张明随机调查了某校若干学生和家长对中学生带手机现象的看法,制作了如图所示的统计图:
(1)这次调查的总人数有_____人;
(2)补全两个统计图;
(3)针对随机调查的情况,张明决定从初三一班表示赞成的4位家长中随机选择2位进行深入调查,其中包含小亮和小明的家长,小亮和小明的家长被同时选中的概率是_____.(以上三个问题均不需写过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),其表达式是y=ax2+c的形式.请根据所给的数据求出a,c的值.
(2)求支柱MN的长度.
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说说你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ACB=90°,CD是中线,AC=BC,一个以点D为顶点的45°角绕点D旋转,使角的两边分别与AC、BC的延长线相交,交点分别为点E,F,DF与AC交于点M,DE与BC交于点N.

(1)如图1,若CE=CF,求证:DE=DF;
(2)如图2,在∠EDF绕点D旋转的过程中:
①探究三条线段AB,CE,CF之间的数量关系,并说明理由;
②若CE=4,CF=2,求DN的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“垃圾分一分,明天美十分”.环保部门计划订制一批垃圾分类宣传海报,海报版面不小于300平方米,当宣传海报的版面为300平方米时,价格为80元/平方米.为了支持垃圾分类促进环保,广告公司给予以下优惠:宣传海报版面每增加1平方米,每平方米的价格减少0.2元,但不能低于50元/平方米.假设宣传海报的版面增加![]() 平方米后,总费用为
平方米后,总费用为![]() 元.
元.
(1)求![]() 关于
关于![]() 的函数表达式;
的函数表达式;
(2)订制宣传海报的版面为多少平方米时总费用最高?最高费用为多少元?
(3)环保部门希望总费用尽可能低,那么应该订制多少平方米的海报?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com