
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() НЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯп
НЛxжсгкAЃЌBСНЕуЃЌНЛyжсгкЕуCЃЎжБЯп![]() ОЙ§ЕуAЃЌCЃЎ
ОЙ§ЕуAЃЌCЃЎ
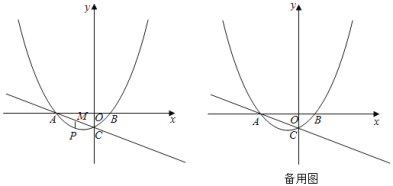
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧХзЮяЯпЩЯвЛЖЏЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпЃЌНЛжБЯпACгкЕуMЃЌЩшЕуPЕФКсзјБъЮЊmЃЎ
ЂйЕБ![]() ЪЧжБНЧШ§НЧаЮЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЪЧжБНЧШ§НЧаЮЪБЃЌЧѓЕуPЕФзјБъЃЛ
ЂкзїЕуBЙигкЕуCЕФЖдГЦЕу![]() ЃЌдђЦНУцФкДцдкжБЯпlЃЌЪЙЕуMЃЌBЃЌ
ЃЌдђЦНУцФкДцдкжБЯпlЃЌЪЙЕуMЃЌBЃЌ![]() ЕНИУжБЯпЕФОрРыЖМЯрЕШЃЎЕБЕуPдкyжсгвВрЕФХзЮяЯпЩЯЃЌЧвгыЕуBВЛжиКЯЪБЃЌЧыжБНгаДГіжБЯп
ЕНИУжБЯпЕФОрРыЖМЯрЕШЃЎЕБЕуPдкyжсгвВрЕФХзЮяЯпЩЯЃЌЧвгыЕуBВЛжиКЯЪБЃЌЧыжБНгаДГіжБЯп![]() ЕФНтЮіЪНЃЎЃЈkЃЌbПЩгУКЌmЕФЪНзгБэЪОЃЉ
ЕФНтЮіЪНЃЎЃЈkЃЌbПЩгУКЌmЕФЪНзгБэЪОЃЉ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЈ2ЃЉЂй
ЃЈ2ЃЉЂй![]() Лђ
Лђ![]() ЃЌЂкжБЯпlЕФНтЮіЪНЮЊ
ЃЌЂкжБЯпlЕФНтЮіЪНЮЊ![]() ,
,![]() Лђ
Лђ![]() .
.
ЁОНтЮіЁП
ЃЈ1ЃЉРћгУвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуAЃЌCЕФзјБъЃЌИљОнЕуAЃЌCЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіЖўДЮКЏЪ§НтЮіЪНЃЛ
ЃЈ2ЃЉЂйгЩPMЁЭxжсПЩЕУГіЁЯPMCЁй90ЁуЃЌЗжЁЯMPC=90ЁуМАЁЯPCM=90ЁуСНжжЧщПіПМТЧЃКЃЈiЃЉЕБЁЯMPC=90ЁуЪБЃЌPCЁЮxжсЃЌРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЧѓГіЕуPЕФзјБъЃЛЃЈiiЃЉЕБЁЯPCM=90ЁуЪБЃЌЩшPCгыxжсНЛгкЕуDЃЌвзжЄЁїAOCЁзЁїCODЃЌРћгУЯрЫЦШ§НЧаЮЕФаджЪПЩЧѓГіЕуDЕФзјБъЃЌИљОнЕуCЃЌDЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіжБЯпPCЕФНтЮіЪНЃЌСЊСЂжБЯпPCКЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЭЈЙ§НтЗНГЬзщПЩЧѓГіЕуPЕФзјБъЃЎзлЩЯЃЌДЫЮЪЕУНтЃЛ
ЂкРћгУЖўДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїМАвЛДЮКЏЪ§ЭМЯѓЩЯЕуЕФзјБъЬиеїПЩЕУГіЕуBЃЌMЕФзјБъЃЌНсКЯЕуCЕФзјБъПЩЕУГіЕуBЁфЕФзјБъЃЌИљОнЕуMЃЌBЃЌBЁфЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈПЩЗжБ№ЧѓГіжБЯпBMЃЌBЁфMКЭBBЁфЕФНтЮіЪНЃЌРћгУЦНааЯпЕФаджЪПЩЧѓГіжБЯпlЕФНтЮіЪНЃЎ
НтЃКЃЈ1ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
![]() ЕуCЕФзјБъЮЊ
ЕуCЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
![]() ЕуAЕФзјБъЮЊ
ЕуAЕФзјБъЮЊ![]() ЃЎ
ЃЎ
НЋ![]() ЃЌ
ЃЌ![]() ДњШы
ДњШы![]() ЃЌЕУЃК
ЃЌЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК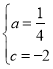 ЃЌ
ЃЌ
![]() ХзЮяЯпЕФНтЮіЪНЮЊ
ХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂй![]() жсЃЌ
жсЃЌ
![]() ЃЌ
ЃЌ
![]() ЗжСНжжЧщПіПМТЧЃЌШчЭМ1ЫљЪОЃЎ
ЗжСНжжЧщПіПМТЧЃЌШчЭМ1ЫљЪОЃЎ
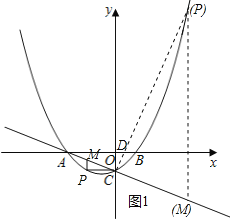
ЃЈiЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() жсЃЌ
жсЃЌ
![]() ЕуPЕФзнзјБъЮЊЉ2ЃЎ
ЕуPЕФзнзјБъЮЊЉ2ЃЎ
ЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЕуPЕФзјБъЮЊ
ЕуPЕФзјБъЮЊ![]() ЃЛ
ЃЛ
ЃЈiiЃЉЕБ![]() ЪБЃЌЩшPCгыxжсНЛгкЕуDЃЎ
ЪБЃЌЩшPCгыxжсНЛгкЕуDЃЎ
![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ
![]() ЃЎ
ЃЎ
гж![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЃЌМД
ЃЌМД![]() ЃЌ
ЃЌ
![]() ЃЌ
ЃЌ
![]() ЕуDЕФзјБъЮЊ
ЕуDЕФзјБъЮЊ![]() ЃЎ
ЃЎ
ЩшжБЯпPCЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
НЋ![]() ЃЌ
ЃЌ![]() ДњШы
ДњШы![]() ЃЌЕУЃК
ЃЌЕУЃК
![]() ЃЌНтЕУЃК
ЃЌНтЕУЃК![]() ЃЌ
ЃЌ
![]() жБЯпPCЕФНтЮіЪНЮЊ
жБЯпPCЕФНтЮіЪНЮЊ![]() ЃЎ
ЃЎ
СЊСЂжБЯпPCКЭХзЮяЯпЕФНтЮіЪНГЩЗНГЬзщЃЌЕУЃК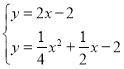 ЃЌ
ЃЌ
НтЕУЃК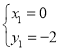 ЃЌ
ЃЌ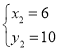 ЃЌ
ЃЌ
ЕуPЕФзјБъЮЊ![]() ЃЎ
ЃЎ
злЩЯЫљЪіЃКЕБ![]() ЪЧжБНЧШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊ
ЪЧжБНЧШ§НЧаЮЪБЃЌЕуPЕФзјБъЮЊ![]() Лђ
Лђ![]() ЃЎ
ЃЎ
ЂкЕБy=0ЪБЃЌ![]() ,
,
НтЕУЃКx1=-4ЃЌx2=2ЃЌ
ЁрЕуBЕФзјБъЮЊЃЈ2ЃЌ0ЃЉЃЎ
ЁпЕуCЕФзјБъЮЊЃЈ0ЃЌ-2ЃЉЃЌЕуBЃЌBЁфЙигкЕуCЖдГЦЃЌ
ЁрЕуBЁфЕФзјБъЮЊЃЈ-2ЃЌ-4ЃЉЃЎ
ЁпЕуPЕФКсзјБъЮЊmЃЈmЃО0ЧвmЁй2ЃЉЃЌ
ЁрЕуMЕФзјБъЮЊ![]() ,
,
РћгУД§ЖЈЯЕЪ§ЗЈПЩЧѓГіЃКжБЯпBMЕФНтЮіЪНЮЊ![]() ЃЌжБЯпBЁфMЕФНтЮіЪНЮЊ
ЃЌжБЯпBЁфMЕФНтЮіЪНЮЊ![]() ЃЌжБЯпBBЁфЕФНтЮіЪНЮЊy=x-2ЃЎ
ЃЌжБЯпBBЁфЕФНтЮіЪНЮЊy=x-2ЃЎ
ЗжШ§жжЧщПіПМТЧЃЌШчЭМ2ЫљЪОЃК
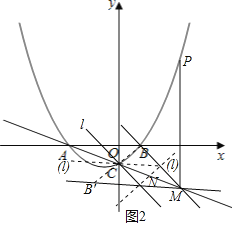
ЕБжБЯпlЁЮBMЧвЙ§ЕуCЪБЃЌжБЯпlЕФНтЮіЪНЮЊ![]() ,
,
ЕБжБЯпlЁЮBЁфMЧвЙ§ЕуCЪБЃЌжБЯпlЕФНтЮіЪНЮЊ![]() ,
,
ЕБжБЯпlЁЮBBЁфЧвЙ§ЯпЖЮCMЕФжаЕу![]() ЪБЃЌжБЯпlЕФНтЮіЪНЮЊ
ЪБЃЌжБЯпlЕФНтЮіЪНЮЊ![]() ,
,
злЩЯЫљЪіЃКжБЯпlЕФНтЮіЪНЮЊ![]() ,
,![]() Лђ
Лђ![]() .
.


 УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ
УћЪІжИЕМЦкФЉГхДЬОэЯЕСаД№АИ ПЊаФЭмПкЫуЬтПЈЯЕСаД№АИ
ПЊаФЭмПкЫуЬтПЈЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ4ЗжЃЉвЛдЊЖўДЮЗНГЬ![]() ЕФИљЕФЧщПіЪЧЃЈ ЃЉ
ЕФИљЕФЧщПіЪЧЃЈ ЃЉ
AЃЎгаСНИіВЛЯрЕШЕФЪЕЪ§Иљ BЃЎгаСНИіЯрЕШЕФЪЕЪ§Иљ
CЃЎУЛгаЪЕЪ§Иљ DЃЎЮоЗЈШЗЖЈ
ЁОД№АИЁПAЃЎ
ЁОНтЮіЁП
ЪдЬтЁпЁї=![]() ЃЌЁрЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎЙЪбЁAЃЎ
ЃЌЁрЗНГЬгаСНИіВЛЯрЕШЕФЪЕЪ§ИљЃЎЙЪбЁAЃЎ
ПМЕуЃКИљЕФХаБ№ЪНЃЎ
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
9
ЁОЬтФПЁПвбжЊжБЯпy=kxЃЈkЃО0ЃЉгыЫЋЧњЯп![]() НЛгкЕуAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉСНЕуЃЌдђx1y2+x2y1ЕФжЕЮЊЁО ЁП
НЛгкЕуAЃЈx1ЃЌy1ЃЉЃЌBЃЈx2ЃЌy2ЃЉСНЕуЃЌдђx1y2+x2y1ЕФжЕЮЊЁО ЁП
AЃЎЉ6 BЃЎЉ9 CЃЎ0 DЃЎ9
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃЦпФъМЖ6ИіАрЕФ180УћбЇЩњМДНЋВЮМгББОЉЪажабЇЩњПЊЗХадПЦбЇЪЕМљЛюЖЏЫЭПЮЕНаЃПЮГЬЕФбЇЯАЃЎбЇЯАФкШнАќРЈвдЯТ7ИіСьгђЃКAЃЎздШЛгыЛЗОГЃЌBЃЎНЁПЕгыАВШЋЃЌCЃЎНсЙЙгыЛњаЕЃЌDЃЎЕчзггыПижЦЃЌEЃЎЪ§ОнгыаХЯЂЃЌFЃЎФмдДгыВФСЯЃЌGЃЎШЫЮФгыРњЪЗЃЎЮЊСЫНтбЇЩњЯВЛЖЕФПЮГЬСьгђЃЌбЇЩњЛсПЊеЙСЫвЛДЮЕїВщбаОПЃЌЧыНЋЯТУцЕФЙ§ГЬВЙШЋЃЎ
ЪеМЏЪ§ОнбЇЩњЛсМЦЛЎЕїВщ30УћбЇЩњЯВЛЖЕФПЮГЬСьгђзїЮЊбљБОЃЌЯТУцГщбљЕїВщЕФЖдЯѓбЁдёКЯРэЕФЪЧЁЁЁЁЃЛЃЈЬюађКХЃЉ
ЂйбЁдёЦпФъМЖ1АрЁЂ2АрИї15УћбЇЩњзїЮЊЕїВщЖдЯѓ
ЂкбЁдёЛњЦїШЫЩчЭХЕФ30УћбЇЩњзїЮЊЕїВщЖдЯѓ
ЂлбЁдёИїАрбЇКХЮЊ6ЕФБЖЪ§ЕФ30УћбЇЩњзїЮЊЕїВщЖдЯѓ
ЕїВщЖдЯѓШЗЖЈКѓЃЌЕїВщаЁзщЛёЕУСЫ30УћбЇЩњЯВЛЖЕФПЮГЬСьгђШчЯТЃК
AЃЌCЃЌDЃЌDЃЌGЃЌGЃЌFЃЌEЃЌBЃЌGЃЌ
CЃЌCЃЌGЃЌDЃЌBЃЌAЃЌGЃЌFЃЌFЃЌAЃЌ
GЃЌBЃЌFЃЌGЃЌEЃЌGЃЌAЃЌBЃЌGЃЌG
ећРэЁЂУшЪіЪ§ОнећРэЁЂУшЪібљБОЪ§ОнЃЌЛцжЦЭГМЦЭМБэШчЯТЃЌЧыВЙШЋЭГМЦБэКЭЭГМЦЭМЃЎ
ФГаЃЦпФъМЖбЇЩњЯВЛЖЕФПЮГЬСьгђЭГМЦБэ
ПЮГЬСьгђ | ШЫЪ§ |
A | 4 |
B | 4 |
C | 3 |
D | 3 |
E | 2 |
F | ЁЁ4ЁЁ |
G | ЁЁ10ЁЁ |
КЯМЦ | 30 |
ЗжЮіЪ§ОнЁЂЭЦЖЯНсТлЧыФуИљОнЩЯЪіЕїВщНсЙћЯђбЇаЃЭЦМіБОДЮЫЭПЮЕНаЃЕФПЮГЬСьгђЃЌФуЕФЭЦМіЪЧЁЁЁЁЃЈЬюAЉGЕФзжФИДњКХЃЉЃЌЙРМЦШЋФъМЖДѓдМгаЁЁЁЁУћбЇЩњЯВЛЖетИіПЮГЬСьгђЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
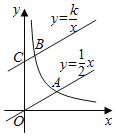
ЁОЬтФПЁПШчЭМЃЌжБЯпyЃН![]() xгыЫЋЧњЯпyЃН
xгыЫЋЧњЯпyЃН![]() ЃЈkЃО0ЃЌxЃО0ЃЉНЛгкЕуAЃЌНЋжБЯпyЃН
ЃЈkЃО0ЃЌxЃО0ЃЉНЛгкЕуAЃЌНЋжБЯпyЃН![]() xЯђЩЯЦНвЦ2ИіЕЅЮЛГЄЖШКѓЃЌгыyжсНЛгкЕуCЃЌгыЫЋЧњЯпНЛгкЕуBЃЌШєOAЃН3BCЃЌдђkЕФжЕЮЊ____ЃЎ
xЯђЩЯЦНвЦ2ИіЕЅЮЛГЄЖШКѓЃЌгыyжсНЛгкЕуCЃЌгыЫЋЧњЯпНЛгкЕуBЃЌШєOAЃН3BCЃЌдђkЕФжЕЮЊ____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
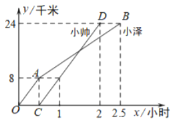
ЁОЬтФПЁПаЁдѓКЭаЁЫЇСНЭЌбЇЗжБ№ДгМзЕиГіЗЂЃЌЦяздааГЕбиЭЌвЛЬѕТЗЕНввЕиВЮМгЩчЛсЪЕМљЛюЖЏЃЎШчЭМелЯп![]() КЭЯпЖЮ
КЭЯпЖЮ![]() ЗжБ№БэЪОаЁдѓКЭаЁЫЇРыМзЕиЕФОрРы
ЗжБ№БэЪОаЁдѓКЭаЁЫЇРыМзЕиЕФОрРы![]() ЃЈЕЅЮЛЃКЧЇУзЃЉгыЪБМф
ЃЈЕЅЮЛЃКЧЇУзЃЉгыЪБМф![]() ЃЈЕЅЮЛЃКаЁЪБЃЉжЎМфКЏЪ§ЙиЯЕЕФЭМЯѓЃЌдђЕБаЁЫЇЕНДяввЕиЪБЃЌаЁдѓОрввЕиЕФОрРыЮЊ_________ЧЇУзЃЎ
ЃЈЕЅЮЛЃКаЁЪБЃЉжЎМфКЏЪ§ЙиЯЕЕФЭМЯѓЃЌдђЕБаЁЫЇЕНДяввЕиЪБЃЌаЁдѓОрввЕиЕФОрРыЮЊ_________ЧЇУзЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
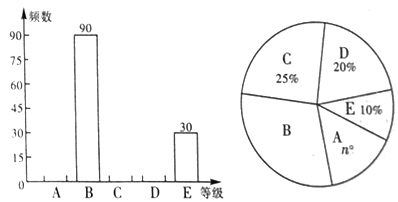
ЁОЬтФПЁП2019Фъ3дТ25ШеЪЧШЋЙњжааЁбЇЩњАВШЋНЬг§ШеЃЌЧАНјжабЇЮЊМгЧПбЇЩњЕФАВШЋвтЪЖЃЌзщШЋаЃбЇЩњВЮМгАВШЋжЊЪЖОКШќЃЌДгжаГщШЁСЫВПЗжбЇЩњГЩМЈ(ЕУЗжШЁе§ећЪ§ЃЌТњЗжЮЊ100Зж)ЃЌИїЕШМЖНјааЭГМЦ(![]() МЖЃЎ
МЖЃЎ![]() Зж-
Зж-![]() ЗжЃЛ
ЗжЃЛ![]() МЖЃЎ
МЖЃЎ![]() Зж
Зж![]() ЗжЃЛ
ЗжЃЛ![]() МЖЃЎ
МЖЃЎ![]() Зж
Зж![]() ЗжЃЛ
ЗжЃЛ![]() МЖЃЎ
МЖЃЎ![]() Зж
Зж![]() ЗжЃЛ
ЗжЃЛ![]() МЖЃЎ
МЖЃЎ![]() Зж
Зж![]() Зж)ЃЌВЂНЋЭГМЦНсЙћЛцжЦГЩШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЌЧыФуНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
Зж)ЃЌВЂНЋЭГМЦНсЙћЛцжЦГЩШчЯТСНЗљЩаВЛЭъећЕФЭГМЦЭМЃЌЧыФуНсКЯЭМжаЫљИјаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉ![]() _______ЃЎ
_______ЃЎ
ЃЈ2ЃЉВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЃЈ3ЃЉИУаЃЙВга![]() УћбЇЩњЃЎШєГЩМЈдк
УћбЇЩњЃЎШєГЩМЈдк![]() ЗжвдЯТ(КЌ
ЗжвдЯТ(КЌ![]() Зж)ЕФбЇЩњАВШЋвтЪЖВЛЧПЃЌгаД§НјЃЎВНМгЧПАВШЋНЬг§ЃЌдђИУаЃАВШЋвтЪЖВЛЧПЕФбЇЩњдМгаЖрЩйУћ?
Зж)ЕФбЇЩњАВШЋвтЪЖВЛЧПЃЌгаД§НјЃЎВНМгЧПАВШЋНЬг§ЃЌдђИУаЃАВШЋвтЪЖВЛЧПЕФбЇЩњдМгаЖрЩйУћ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЦћГЕВњвЕЕФЗЂеЙЃЌгааЇДйНјЮвЙњЯжДњЛЏНЈЩш.ФГЦћГЕЯњЪлЙЋЫО2016ФъгЏРћ1500ЭђдЊЃЌЕН2018ФъгЏРћ2160ЭђдЊЃЌЧвДг2016ФъЕН2018ФъЃЌУПФъгЏРћЕФФъдіГЄТЪЯрЭЌ.
ЃЈ1ЃЉЧѓУПФъгЏРћЕФФъдіГЄТЪЃЛ
ЃЈ2ЃЉШєИУЙЋЫОгЏРћЕФФъдіГЄТЪМЬајБЃГжВЛБфЃЌФЧУД2019ФъИУЙЋЫОгЏРћФмЗёДяЕН2500ЭђдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП[дФЖСРэНт]
ЮвУЧжЊЕР:![]() ЃЌФЧУД
ЃЌФЧУД![]() НсЙћЕШгкЖрЩйФи?
НсЙћЕШгкЖрЩйФи?
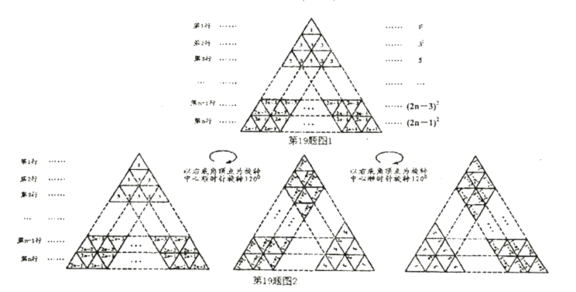
дкЭМ1ЫљЪОЕФЕШБпШ§НЧаЮЪ§еѓжаЃЌЕк![]() ааЕФвЛИіаЁЕШБпШ§НЧаЮжаЕФЪ§ЮЊ
ааЕФвЛИіаЁЕШБпШ§НЧаЮжаЕФЪ§ЮЊ![]() ЃЌМД
ЃЌМД![]() Ек
Ек![]() ааЕФШ§ИіаЁЕШБпШ§НЧаЮжаЕФЪ§ЕФКЭЪЧ
ааЕФШ§ИіаЁЕШБпШ§НЧаЮжаЕФЪ§ЕФКЭЪЧ![]() МД
МД![]() ; ЃЎЃЎЕк
; ЃЎЃЎЕк![]() ааЕФ
ааЕФ![]() ИіаЁЕШБпШ§НЧаЮжаЕФЪ§ЕФКЭЪЧ
ИіаЁЕШБпШ§НЧаЮжаЕФЪ§ЕФКЭЪЧ![]() ИіЃЌМД
ИіЃЌМД![]() ЃЌИУЕШБпШ§НЧаЮЪ§еѓжаЙВга
ЃЌИУЕШБпШ§НЧаЮЪ§еѓжаЙВга![]() аЁЕШБпШ§НЧаЮЃЌЫљгааЁЕШБпШ§НЧаЮЪ§ЕФКЭЮЊ
аЁЕШБпШ§НЧаЮЃЌЫљгааЁЕШБпШ§НЧаЮЪ§ЕФКЭЮЊ![]() ЃЎ
ЃЎ
[ЙцТЩЬНОП]
вдЭМ1жаЕФЕШБпШ§НЧаЮЪ§еѓЕФгвЕзНЧЖЅЕуЮЊа§зЊжааФЫГЪБеыа§зЊ![]() дйАба§зЊКѓЕФЭМаЮАДЭЌбљЕФЗНЗЈПЩЕУШчЭМ2ЫљЪОЕФШ§НЧаЮЪ§еѓЃЌЙлВьетШ§ИіЕШБпШ§НЧаЮЪ§еѓИїааЭЌвЛЮЛжУЕФаЁЕШБпШ§НЧаЮжаЕФЪ§ЃЌЗЂЯжЮЛгкЦцЪ§ЮЛжУЕФШ§ИіЪ§(ШчЕк
дйАба§зЊКѓЕФЭМаЮАДЭЌбљЕФЗНЗЈПЩЕУШчЭМ2ЫљЪОЕФШ§НЧаЮЪ§еѓЃЌЙлВьетШ§ИіЕШБпШ§НЧаЮЪ§еѓИїааЭЌвЛЮЛжУЕФаЁЕШБпШ§НЧаЮжаЕФЪ§ЃЌЗЂЯжЮЛгкЦцЪ§ЮЛжУЕФШ§ИіЪ§(ШчЕк![]() ааЕФЕк
ааЕФЕк![]() ИіаЁШ§НЧаЮжаЕФЪ§ЗжБ№ЮЊ
ИіаЁШ§НЧаЮжаЕФЪ§ЗжБ№ЮЊ![]() ЕФКЭЮЊ
ЕФКЭЮЊ![]() ;ЗЂЯжЮЛгкХМЪ§ЮЛжУЕФШ§ИіЪ§(ШчЕк
;ЗЂЯжЮЛгкХМЪ§ЮЛжУЕФШ§ИіЪ§(ШчЕк![]() ааЕФЕк
ааЕФЕк![]() ИіаЁШ§НЧаЮжаЕФЪ§ЗжБ№ЮЊ
ИіаЁШ§НЧаЮжаЕФЪ§ЗжБ№ЮЊ![]() ЕФКЭЮЊ
ЕФКЭЮЊ![]() ;ЖјУПИіЕШБпШ§НЧаЮЪ§еѓжаЃЌгЩгкЮЛгкЦцЪ§ЮЛжУЕФЪ§БШЮЛгкХМЪ§ЮЛжУЕФЪ§Жр
;ЖјУПИіЕШБпШ§НЧаЮЪ§еѓжаЃЌгЩгкЮЛгкЦцЪ§ЮЛжУЕФЪ§БШЮЛгкХМЪ§ЮЛжУЕФЪ§Жр![]() ИіЃЌдђЮЛгкХМЪ§ЮЛжУЕФЪ§га_
ИіЃЌдђЮЛгкХМЪ§ЮЛжУЕФЪ§га_
Иі![]()
вђДЫЃЌ![]()
[НтОіЮЪЬт]ИљОнвдЩЯЗЂЯжЃЌМЦЫу:![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
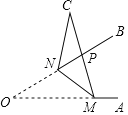
ЁОЬтФПЁПШчЭМЃЌвбжЊЃЌMЃЌNЗжБ№ЮЊШёНЧЁЯAOBЕФБпOAЃЌOBЩЯЕФЕуЃЌON=6ЃЌАбЁїOMNбиMNелЕўЃЌЕуOТфдкЕуCДІЃЌMCгыOBНЛгкЕуPЃЌШєMN=MP=5ЃЌдђPN=(ЁЁЁЁ)
A.2B.3C.![]() D.
D.![]()
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com