
 ��ͼ����ֱ��������ABC�У���ACB=90�㣬AC=8cm��BC=6cm����P�ӵ�A��������4cm/s���ٶ����߶�AB���˶���ͬʱ��QҲ�ӵ�A���������߶�AC�˶�����ʼ�ձ���PQ��AB���Ե�QΪԲ�ģ�PQΪ�뾶����O�����˶�ʱ��Ϊt��s����
��ͼ����ֱ��������ABC�У���ACB=90�㣬AC=8cm��BC=6cm����P�ӵ�A��������4cm/s���ٶ����߶�AB���˶���ͬʱ��QҲ�ӵ�A���������߶�AC�˶�����ʼ�ձ���PQ��AB���Ե�QΪԲ�ģ�PQΪ�뾶����O�����˶�ʱ��Ϊt��s�������� ��1������PQ��AB��ֱ��������ABC�ó�Rt��ACB��Rt��APQ���������PQ�����ù��ɶ����ó�AQ���ɣ�
��2������BC���Q���еó�QC=PQ=3t����AQ+QC=AC����������⼴�ɣ�
��3�����жϳ�Rt��APQ��Rt��QED�������DE���������ε������ʽ�ó�S��CDQ=-$\frac{9}{2}$��t-$\frac{4}{5}$��2+$\frac{72}{25}$������ȷ�������ֵ��
��� �⣺��1��
��PQ��AB����ABC��ֱ�������Σ�
��Rt��ACB��Rt��APQ��
��$\frac{AC}{BC}=\frac{AP}{PQ}$��
���˶�֪��AP=4t��
��AC=8��BC=6��
��$\frac{8}{6}=\frac{4t}{PQ}$��
��PQ=3t��
����ݹ��ɶ����ã�AQ=5t��
���Q���ٶ�Ϊ$\frac{5t}{t}$=5��cm/s����
��2���ߡ�Q��BC���У�
��QC=PQ=3t��
��AC=AQ+QC=8��
��5t+3t=8��
��t=1��
��3����ͼ��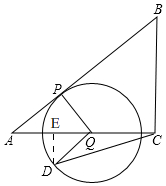 ����D��DE��AC��E��
����D��DE��AC��E��
��QD��AB��PQ��AB��
��Rt��APQ��Rt��QED��
��$\frac{PQ}{AQ}=\frac{DE}{DQ}$��
��PQ=3t��AQ=5t��DQ=PQ=3t��
��$\frac{3t}{5t}=\frac{DE}{3t}$��
��DE=$\frac{9}{5}$t��
��QC=8-5t��
��S��CDQ=$\frac{1}{2}$QC•DE=$\frac{1}{2}$��8-5t��•$\frac{9}{5}$t=-$\frac{9}{2}$��t-$\frac{4}{5}$��2+$\frac{72}{25}$��
��-$\frac{9}{2}$��0����
���CDQ��������ֵΪ$\frac{72}{25}$��
���� ������Բ���ۺ��⣬��Ҫ���������������ε��ж������ʣ����е����ʣ����ɶ������⣨1���Ĺؼ��ǵó�PQ=3t���⣨2���Ĺؼ�����AC=AQ+CQ�������̣��⣨3���Ĺؼ��ǽ��������ε�������˶�ʱ��t�ĺ�����ϵʽ��


 ��Ч���ܿ�ʱ��ҵϵ�д�
��Ч���ܿ�ʱ��ҵϵ�д� �ݾ�ѵ������ϵ�д�
�ݾ�ѵ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | SAS | B�� | AAS | C�� | ASA | D�� | SSS |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
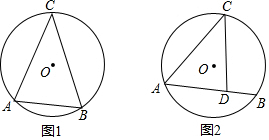
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+6��ͼ��x����A��B���㣬��y���ڵ�D����CΪ�����ߵĶ��㣬��A��B����ĺ�����ֱ�Ϊ1��3��
��ͼ����ƽ��ֱ������ϵ�У����κ���y=ax2+bx+6��ͼ��x����A��B���㣬��y���ڵ�D����CΪ�����ߵĶ��㣬��A��B����ĺ�����ֱ�Ϊ1��3���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a2-b2 | B�� | a2-2a+1 | C�� | ab-a | D�� | a2+b2 |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com