
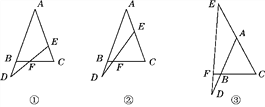
【题目】在等腰三角形ABC中,AB=AC,D是AB延长线上一点,E是AC上一点,DE交BC于点F.
(1)如图①,若BD=CE,求证:DF=EF.
(2)如图②,若BD=![]() CE,试写出DF和EF之间的数量关系,并证明.
CE,试写出DF和EF之间的数量关系,并证明.
(3)如图③,在(2)的条件下,若点E在CA的延长线上,那么(2)中结论还成立吗?试证明.
【答案】(1)证明见解析;(2)DF=![]() EF.(3)成立,证明见解析.
EF.(3)成立,证明见解析.
【解析】试题分析:
(1)在题图①中作EG∥AB交BC于点G,利用平行线的性质和等腰三角形的性质可证得:EG=EC;再证△BFD≌△GFE即可;
(2)在题图②中作EG∥AB交BC于点G,则∠D=∠FEG.同(1)可得EG=EC;
再证△BFD∽△GFE,利用相似三角形的性质即可证得:DF=![]() EF.
EF.
(3)在题图③中作EG∥AB交CB的延长线于点G,同(2)证:EG=EC,△BFD∽△GFE,再利用相似三角形的性质可得:DF=![]() EF,即(2)中的结论任然成立
EF,即(2)中的结论任然成立
试题解析:
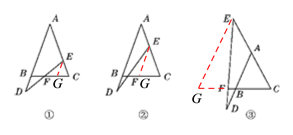
(1)在题图①中作EG∥AB交BC于点G,
则∠ABC=∠EGC,∠D=∠FEG.
∵AB=AC,∴∠ABC=∠C.
∴∠EGC=∠C.∴EG=EC.
∵BD=CE,∴BD=EG.
∵∠D=∠FEG,∠BFD=∠GFE,
∴△BFD≌△GFE.
∴DF=EF.
(2)解:DF=![]() EF.
EF.
在题图②中作EG∥AB交BC于点G,则∠D=∠FEG.由(1)得EG=EC.
∵∠D=∠FEG,∠BFD=∠EFG,
∴△BFD∽△GFE.
∴![]() .
.
∵BD=![]() CE=
CE=![]() EG,
EG,
∴DF=![]() EF.
EF.
(3)成立.
在题图③中作EG∥AB交CB的延长线于点G,
则仍有EG=EC,△BFD∽△GFE.
∴![]() ,
,
∵BD=![]() CE=
CE=![]() EG,
EG,
∴DF=![]() EF.
EF.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在下列条件中,不能作为判断△ABD≌△BAC的条件是( )

A. ∠D=∠C,∠BAD=∠ABC B. ∠BAD=∠ABC,∠ABD=∠BAC
C. BD=AC,∠BAD=∠ABC D. AD=BC,BD=AC
查看答案和解析>>
科目:初中数学 来源: 题型:
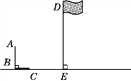
【题目】如图,九年级(1)班的小明与小艳两位同学去操场测量旗杆DE的高度,已知直立在地面上的竹竿AB的长为3 m.某一时刻,测得竹竿AB在阳光下的投影BC的长为2 m.
(1)请你在图中画出此时旗杆DE在阳光下的投影,并写出画图步骤;
(2)在测量竹竿AB的影长时,同时测得旗杆DE在阳光下的影长为6 m,请你计算旗杆DE的高度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
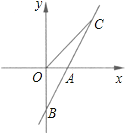
【题目】如图,直线AB与x轴交于点A(1,0),与y轴交于点B(0,﹣2).
(1)求直线AB的解析式;
(2)若直线AB上的点C在第一象限,且S△BOC=2,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】动物学家通过大量的调查估计出,某种动物活到20岁的概率为0.8,活到25岁的概率是0.5,活到30岁的概率是0.3.现年20岁的这种动物活到25岁的概率为多少?现年25岁的这种动物活到30岁的概率为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD和四边形![]() 位似,位似比
位似,位似比![]() =2,四边形A′B′C′D′和四边形
=2,四边形A′B′C′D′和四边形![]() 位似,位似比
位似,位似比![]() =1.四边形
=1.四边形![]() 和四边形ABCD是位似图形吗?位似比是多少?
和四边形ABCD是位似图形吗?位似比是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仔细阅读材料,再尝试解决问题:
完全平方式![]() 以及
以及![]() 的值为非负数的特点在数学学习中有广泛的应用,比如探求
的值为非负数的特点在数学学习中有广泛的应用,比如探求![]() 的最大(小)值时,我们可以这样处理:
的最大(小)值时,我们可以这样处理:
解:原式 = ![]() .
.
因为无论![]() 取什么数,都有
取什么数,都有![]() 的值为非负数,所以
的值为非负数,所以![]() 的最小值为0;此时
的最小值为0;此时![]() 时,进而
时,进而![]() 的最小值是
的最小值是![]() ;所以当
;所以当![]() 时,原多项式的最小值是
时,原多项式的最小值是![]() .
.
请根据上面的解题思路,探求:
⑴.多项式![]() 的最小值是多少,并写出对应的
的最小值是多少,并写出对应的![]() 的取值;
的取值;
⑵.多项式![]() 的最大值是多少,并写出对应的
的最大值是多少,并写出对应的![]() 的取值.
的取值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com