
【题目】在锐角![]() 中,
中,![]() ,
,![]() ,
,![]() ,将
,将![]() 绕点
绕点![]() 按逆时针方向旋转,得到
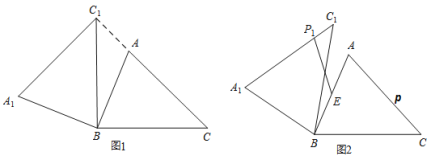
按逆时针方向旋转,得到![]() .(1)如图1,当点
.(1)如图1,当点![]() 在线段
在线段![]() 的延长线上时,则
的延长线上时,则![]() 的度数为______________度;(2)如图2,点
的度数为______________度;(2)如图2,点![]() 为线段
为线段![]() 中点,点
中点,点![]() 是线段
是线段![]() 上的动点,在
上的动点,在![]() 绕点
绕点![]() 按逆时针方向旋转过程中,点
按逆时针方向旋转过程中,点![]() 的对应点是点
的对应点是点![]() ,则线段
,则线段![]() 长度最小值是_____________.
长度最小值是_____________.
科目:初中数学 来源: 题型:
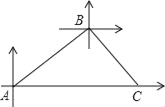
【题目】甲、乙两条轮船同时从港口A出发,甲轮船以每小时30海里的速度沿着北偏东60°的方向航行,乙轮船以每小时15海里的速度沿着正东方向行进,1小时后,甲船接到命令要与乙船会合,于是甲船改变了行进的速度,沿着东南方向航行,结果在小岛C处与乙船相遇.假设乙船的速度和航向保持不变,求:
(1)港口A与小岛C之间的距离;
(2)甲轮船后来的速度.
查看答案和解析>>
科目:初中数学 来源: 题型:
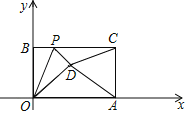
【题目】如图,已知一个矩形纸片OACB,将该纸片放置在平面直角坐标系中,点A(10,0),点B(0,6),点P为BC边上的动点,将△OBP沿OP折叠得到△OPD,连接CD、AD.则下列结论中:①当∠BOP=45°时,四边形OBPD为正方形;②当∠BOP=30°时,△OAD的面积为15;③当P在运动过程中,CD的最小值为2![]() ﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( )
﹣6;④当OD⊥AD时,BP=2.其中结论正确的有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
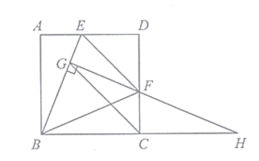
【题目】如图,在正方形![]() 中,
中,![]() 是边
是边![]() 上的动点(与点
上的动点(与点![]() 、
、![]() 不重合),且
不重合),且![]() ,
,![]() 于点
于点![]() ,
,![]() 与
与![]() 的延长线交于点
的延长线交于点![]() ,连接
,连接![]() 、
、![]() .
.
(1)求证:①![]()
![]()
![]() ;②
;②![]() ;
;
(2)若![]() ,在点
,在点![]() 运动过程中,探究:
运动过程中,探究:
①线段![]() 的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
的长度是否改变?若不变,求出这个定值;若改变,请说明理由;
②当![]() 为何值时,
为何值时,![]() 为等腰直角三角形.
为等腰直角三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①是被誉为“川北第一楼”的凤凰楼,它不仅是广元市的城标,更是一份承传文化的载体.李铭和王华同学想借助无人机测量凤凰楼的高度,如图②为测量示意图,他们站在坡度是![]() ,坡面长为
,坡面长为![]() 的斜坡
的斜坡![]() 的坡底
的坡底![]() 处操控无人机,无人机从坡顶
处操控无人机,无人机从坡顶![]() 出发,以
出发,以![]() 的速度,沿仰角
的速度,沿仰角![]() 的方向爬升,
的方向爬升,![]() 时到达空中的
时到达空中的![]() 处.
处.
(1)求此时无人机离坡底![]() 所在地面的高度;
所在地面的高度;
(2)如图②,无人机在![]() 处测得凤凰楼顶部
处测得凤凰楼顶部![]() 的仰角为
的仰角为![]() ,底部
,底部![]() 的俯角为
的俯角为![]() (凤凰楼与李铭和王华所站坡底
(凤凰楼与李铭和王华所站坡底![]() 在同一水平面),求凤凰楼的高度
在同一水平面),求凤凰楼的高度![]() .
.
(结果精确到![]() ;参考数据:
;参考数据:![]() ,
,![]() ,
,![]() ,
,![]() )
)
图① 图②
图②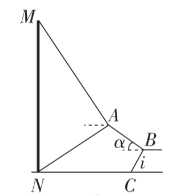
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() 是射线
是射线![]() 上一点,连接
上一点,连接![]() ,沿
,沿![]() 将三角形
将三角形![]() 折叠,得三角形
折叠,得三角形![]() .
.
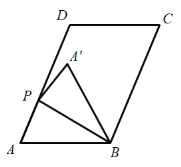
(1)当![]() 时,
时,![]() =_______度;
=_______度;
(2)如图,当![]() 时,求线段
时,求线段![]() 的长度;
的长度;

(3)当点![]() 落在平行四边形
落在平行四边形![]() 的边上时,直接写出线段
的边上时,直接写出线段![]() 的长度.
的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了节省材料,某水产养殖户利用水库的岸堤(岸堤足够长)为一边,用总长为![]() 米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设
米的围网在水库中围成了如图所示的①②③三块矩形区域,而且这三块矩形区域的面积相等.设![]() 的长度为
的长度为![]() 米,矩形区域
米,矩形区域![]() 的面积为
的面积为![]() 米
米![]() .
.
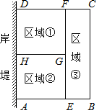
![]() 求证:
求证:![]() ;
;
![]() 求
求![]() 与
与![]() 之间的函数关系式,并写出自变量
之间的函数关系式,并写出自变量![]() 的取值范围;
的取值范围;
![]() 为何值时,
为何值时,![]() 有最大值?最大值是多少?
有最大值?最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】饮料厂生产某品牌的饮料成本是每瓶5元,每天的生产量不超过9000瓶.根据市场调查,以单价8元批发给经销商,经销商每天愿意经销5000瓶,并且表示单价每降价0.1元,经销商每天愿意多经销500瓶.
(1)求出饮料厂每天的利润![]() (元)与批发单价
(元)与批发单价![]() (元)之间的函数关系式;
(元)之间的函数关系式;
(2)批发单价定为多少元时,饮料厂每天的利润最大,最大利润是多少元;
(3)如果该饮料厂要使每天的利润不低于18750元,且每天的总成本不超过42500元,那么批发单价应控制在什么范围.(每天的总成本![]() 每瓶的成本
每瓶的成本![]() 每天的经销量)
每天的经销量)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com