
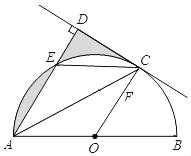
【题目】如图,AB是⊙O的直径,C是半圆O上的一点,AC平分∠DAB如图,AB是
⊙O的直径,C是半圆O上的一点,AC平分∠DAB,AD⊥CD,垂足为D,AD交⊙O于E,连接CE.
(1)判断CD与⊙O的位置关系,并证明你的结论;
(2)若E是弧AC的中点,⊙O的半径为1,求图中阴影部分的面积.
【答案】(1)CD与圆O相切;证明见解析
(2)S阴影=S△DEC=![]() ×
×![]() ×
×![]() =
=![]() .
.
【解析】
试题分析:(1)CD与圆O相切,理由如下:由AC为角平分线得到一对角相等,利用等角对等边得到一对角相等,等量代换得到一对内错角相等,利用内错角相等两直线平行得到OC与AD平行,进而得到OC与CD垂直,即可得证;
(2)连接EB,交OC于F,利用直径所对的圆周角为直角,以及切线的性质,得到一对直角相等,利用同位角相等两直线平行得到OC与AD平行,由O为AB中点,得到F为BE中点,利用中位线定理求出OF的长,进而利用勾股定理求出EF的长,阴影部分面积等于三角形EDC面积,求出即可.
试题解析:(1)CD与圆O相切,理由如下:
∵AC为∠DAB的平分线,
∴∠DAC=∠BAC,
∵OA=OC,
∴∠OAC=∠OCA,
∴∠DAC=∠OCA,
∴OC∥AD,
∵AD⊥CD,
∴OC⊥CD,
则CD与圆O相切;
(2)连接EB,交OC于F,
∵AB为直径,
∴∠AEB=90°,
∴EB∥CD,
∵CD与⊙O相切,C为切点,
∴OC⊥CD,
∴OC∥AD,
∵点O为AB的中点,
∴OF为△ABE的中位线,
∴OF=![]() AE=
AE=![]() ,即CF=DE=
,即CF=DE=![]() ,
,
在Rt△OBF中,根据勾股定理得:EF=FB=DC=![]() ,
,
则S阴影=S△DEC=![]() ×
×![]() ×
×![]() =
=![]() .
.


科目:初中数学 来源: 题型:
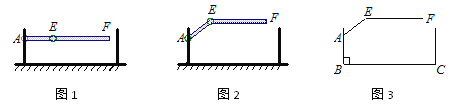
【题目】某地下车库出口处安装了“两段式栏杆”,如图1所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC, EF∥BC,∠AEF=143°,AB=AE=1.3米,那么适合该地下车库的车辆限高标志牌为多少米?(结果精确到0.1.参考数据:sin 37° ≈ 0.60,cos 37° ≈ 0.80,tan 37° ≈ 0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,真命题是( )
A. 如果|a|=|b|,那么a=b
B. 三角形的外角一定大于三角形的内角
C. 直角三角形的两个锐角互余
D. 一个角的余角一定小于这个角
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一批货物要运往某地,货主准备租用汽车运输公司的甲、乙两种货车.已知过去两次租用这两种货车的情况如下表:
第一次 | 第二次 | |
甲种货车辆数(辆) | 2 | 5 |
乙种货车辆数(辆) | 3 | 6 |
累计运货吨数(吨) | 15.5 | 35 |
现租用该公司3辆甲种货车及5辆乙种货车一次刚好运完这批货,如果按每吨付运费30元计算,问货主应付运费多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次抽样调查中收集了一些数据,对数据进行分组,绘制了频数分布表,由于操作失误,绘制时不慎把第三小组的频数弄丢了,现在只知道最后一组(89.5~99.5)出现的百分比为15%,由此可知丢失的第三小组的频数是。
分组 | 49.5~59.5 | 59.5~69.5 | 69.5~79.5 | 79.5~89.5 | 89.5~99.5 |
频数 | 9 | 15 | ? | 16 | 12 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com