Question

如图，在△ABC中，D、E分别是AB、AC的中点，BE=2DE，延长DE到点F，使得EF=BE，连接CF．
（1）求证：四边形BCFE是菱形；
（2）若CE=4，∠BCF=120°，求菱形BCFE的面积．

 

 

Answer 1

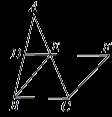
（1）证明：∵D、E分别是AB、AC的中点，
∴DE∥BC且2DE=BC，
又∵BE=2DE，EF=BE，
∴EF=BC，EF∥BC，
∴四边形BCFE是平行四边形，
又∵BE=FE，
∴四边形BCFE是菱形；
（2）【解析】
∵∠BCF=120°，
∴∠EBC=60°，
∴△EBC是等边三角形，
∴菱形的边长为4，高为2，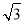
∴菱形的面积为4×2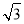=8．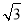

 

【解析】

从所给的条件可知，DE是△ABC中位线，所以DE∥BC且2DE=BC，所以BC和EF平行且相等，所以四边形BCFE是平行四边形，又因为BE=FE，所以是菱形；∠BCF是120°，所以∠EBC为60°，所以菱形的边长也为4，求出菱形的高面积就可求．