
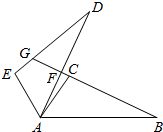
 如图,△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,则∠DFB=90°.
如图,△ABC≌△ADE,∠CAD=10°,∠B=25°,∠EAB=120°,则∠DFB=90°. 科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
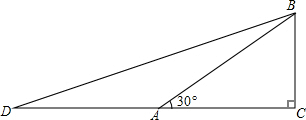 若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?
若想求cos15°的值,可先画Rt△ABC,使∠C=90°,∠BAC=30°,再延长CA到D,使DA=AB,连结BD.利用这些条件,你能否求出tan15°的值?查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
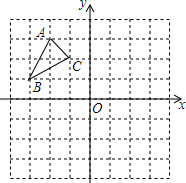 如图,△ABC中A(-2,3),B(-31),C(-1,2).
如图,△ABC中A(-2,3),B(-31),C(-1,2).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com