
【题目】已知二次函数![]() 的部分图象如图所示,则关于
的部分图象如图所示,则关于![]() 的一元二次方程
的一元二次方程![]() 的解为 .
的解为 .

【答案】x1=-1或x2=3.
【解析】试题分析:由二次函数y=-x2+2x+m的部分图象可以得到抛物线的对称轴和抛物线与x轴的一个交点坐标,然后可以求出另一个交点坐标,再利用抛物线与x轴交点的横坐标与相应的一元二次方程的根的关系即可得到关于x的一元二次方程-x2+2x+m=0的解.
试题解析:依题意得二次函数y=-x2+2x+m的对称轴为x=1,与x轴的一个交点为(3,0),
∴抛物线与x轴的另一个交点横坐标为1-(3-1)=-1,
∴交点坐标为(-1,0)
∴当x=-1或x=3时,函数值y=0,
即-x2+2x+m=0,
∴关于x的一元二次方程-x2+2x+m=0的解为x1=-1或x2=3.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读下列一段文字,然后回答下列问题.
已知在平面内两点P1(x1 , y1)、P2(x2 , y2),其两点间的距离 ![]() ,
,
同时,当两点所在的直线在坐标轴或平行于坐标轴或垂直于坐标轴时,两点间距离公式可简化为|x2﹣x1|或|y2﹣y1|.
(1)已知A(2,4)、B(﹣3,﹣8),试求A、B两点间的距离;
(2)已知A、B在平行于y轴的直线上,点A的纵坐标为4,点B的纵坐标为﹣1,试求A、B两点间的距离;
(3)已知一个三角形各顶点坐标为D(1,6)、E(﹣2,2)、F(4,2),你能判定此三角形的形状吗?说明理由;
(4)平面直角坐标中,在x轴上找一点P,使PD+PF的长度最短,求出点P的坐标以及PD+PF的最短长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文艺团体为“希望工程”募捐组织了一场义演,共售出2000张票,筹得票款13600元.已知学生票5元/张,成人票8元/张,问成人票与学生票各售出多少张?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票价格如表:
购票人数/人 | 1~50 | 51~100 | 100以上 |
每人门票价/元 | 12 | 10 | 8 |
某校七年级(1)、(2)两班计划去游览该景点,其中(1)班人数少于50人,(2)班人数多于50人且少于100人,如果两班都以班为单位单独购票,则一共支付1118元;如果两班联合起来作为一个团体购票,则只需花费816元.
(1)两个班各有多少名学生?
(2)团体购票与单独购票相比较,两个班各节约了多少钱?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
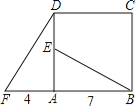
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数 ![]() (x<0)图象上一点,AO的延长线交函数
(x<0)图象上一点,AO的延长线交函数 ![]() (x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于
(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com