
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数 ![]() (x<0)图象上一点,AO的延长线交函数
(x<0)图象上一点,AO的延长线交函数 ![]() (x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于
(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于
【答案】10
【解析】过A作AD⊥x轴于D,连接OA′,
∵点A是函数y= ![]() (x<0)图象上一点,
(x<0)图象上一点,
∴设A(a, ![]() ),
),
∵点C在函数y= ![]() (x>0,k是不等于0的常数)的图象上,
(x>0,k是不等于0的常数)的图象上,
∴设C(b, ![]() ),
),
∵AD⊥BD,BC⊥BD,
∴△OAD∽△BCO,
∴S△ADOS△BCO=( ![]() ) =
) = ![]() ,
,
∵S△ADO= ![]() ,S△BOC=
,S△BOC= ![]() ,
,
∴k =( ![]() ) ,
) ,
∵S△ABC=S△AOB+S△BOC= ![]() (
( ![]() )b+
)b+ ![]() =6,
=6,
∴k ![]() =12,①当k>0时,
=12,①当k>0时,
k= ![]() ,
,
∴k+k12=0,
解得:k=3,k=4(不合题意舍去),②当k<0时,
k=,
∴k+k12=0,
解得:k=3,k=4(不合题意舍去),
∴k=9
∵点A关于y轴的对称点为A′,点C关于x轴的对称点为C′,
∴∠1=∠2,∠3=∠4,
∴∠1+∠4=∠2+∠3=90°,
∴OA′,OC′在同一条直线上,
∴S△OBC′=S△OBC= ![]() =
= ![]() ,
,
∵S△OAA′=2S△OAD=1,
∴由线段AC,CC′,C′A′,A′A所围成的图形的面积=S△OBC+S△OBC′+S△OAA′=10.
故答案为:10.
不规则图形面积可转化为规则图形面积的和,即所围成的图形的面积=S△OBC+S△OBC′+S△OAA′,分别计算三角形面积求和即可.


科目:初中数学 来源: 题型:
【题目】现有2cm,3cm,5cm,7cm长的四条线段,任取其中三条,可以组成的三角形的情况个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】太阳的半径约为696300km.696 300这个数用科学记数法可表示为( )
A.0.696 3×106
B.6.963×105
C.69.63×104
D.696.3×103
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.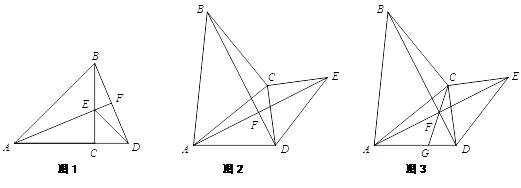
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5.
①求证:AF⊥BD,
②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时.求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数,若不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com