
【题目】在△ABC和△DEC中,AC=BC,DC=EC,∠ACB=∠ECD=90°.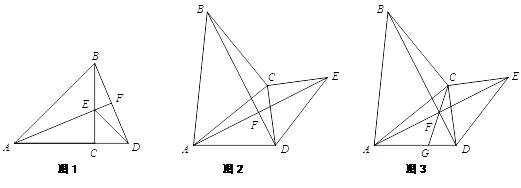
(1)如图1,当点A、C、D在同一条直线上时,AC=12,EC=5.
①求证:AF⊥BD,
②求AF的长度;
(2)如图2,当点A、C、D不在同一条直线上时.求证:AF⊥BD;
(3)如图3,在(2)的条件下,连接CF并延长CF交AD于点G,∠AFG是一个固定的值吗?若是,求出∠AFG的度数,若不是,请说明理由.
【答案】
(1)①证明:如图1,
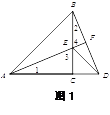
∵AC=BC,∠ACB=∠ECD=90°,EC=DC,∴△ACE≌△BCD,
∴∠1=∠2,∵∠3=∠4,∴∠BFE=∠ACE=90°,∴AF⊥BD.
②解:∵∠ECD=90°,BC= AC=12,DC= EC=5,∴BD=13,
∵S△ABD= ![]() AD·BC=
AD·BC= ![]() BD·AF,∴AF=
BD·AF,∴AF= ![]() .
.
(法2:∵∠ECD=90°,BC= AC=12,DC= EC=5,∴AE=BD=13,BE=7,设EF=x,
∵∠BFE=90°,∴BF2=BE2-EF2,BF2=AB2-AF2,∴72-x2=288-(13+x)2,
∴x= ![]() ,∴AF=13+
,∴AF=13+ ![]() =
= ![]() .)
.)
(2)证明:如图4,∵∠ACB=∠ECD,∴∠ACB+∠ACD=∠ECD+∠ACD,∴∠BCD=∠ACE,
∵AC=BC,∠ACE=∠BCD,EC=DC,∴△ACE≌△BCD,∴∠1=∠2,
∵∠3=∠4,∴∠BFA=∠BCA=90°,∴AF⊥BD.
(3)解:∠AFG=45°.
如图4,
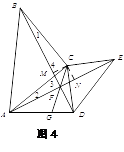
过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,
∵△ACE≌△BCD,∴S△ACE=S△BCD,AE=BD,∵S△ACE= ![]() AE·CN,
AE·CN,
S△BCD= ![]() BD·CM,∴,
BD·CM,∴,
∵CM⊥BD,CN⊥AE,∴CF平分∠BFE,
∵AF⊥BD,∴∠BFE=90°,∴∠EFC=45°,∴∠AFG=45°.
(法2:过点C作CM⊥BD,CN⊥AE,垂足分别为M、N,∵CM⊥BD,CN⊥AE,
∴∠BMC=∠ANC=90°,∵△ACE≌△BCD,∴∠1=∠2,∵∠BMC=∠ANC=90°,∠1=∠2,
AC=BC,∴△BCM≌△ACN,∴CM=CN,∵CM⊥BD,CN⊥AE,∴CF平分∠BFE,
∵AF⊥BD,∴∠BFE=90°,∴∠EFC=45°,∴∠AFG=45°.)
【解析】(1)①由题中标志性条件”AC=BC,EC=DC“可证△ACE≌△BCD,对应角相等,进而可证出垂直;②利用的结论转化AE=BD,EC=ED,利用面积法求出AF的长;(2)借鉴(1)的思路方法,仍然证△ACE≌△BCD,进而证出AF⊥BD;(3)由(2)的结论,可根据面积相等,底边相等,则高相等,即到角两边距离相等的点在这个角的平分线上,得出CF平分∠BFE,进而得出∠AFG=45°.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:
【题目】(本题6分)甲、乙两人进行摸牌游戏.现有三张形状大小完全相同的牌,正面分别标有数字2,3,5.将三张牌背面朝上,洗匀后放在桌子上.
(1)甲从中随机抽取一张牌,记录数字后放回洗匀,乙再随机抽取一张.请用列表法或画树状图的方法,求两人抽取相同数字的概率;
(2)若两人抽取的数字和为2的倍数,则甲获胜;若抽取的数字和为5的倍数,则乙获胜.这个游戏公平吗?请用概率的知识加以解释.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD是正方形,△ADF旋转一定角度后得到△ABE,如图所示,如果AF=4,AB=7,
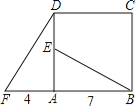
(1)指出旋转中心和旋转角度;
(2)求DE的长度;
(3)BE与DF的位置关系如何?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,O是坐标原点,点A是函数 ![]() (x<0)图象上一点,AO的延长线交函数
(x<0)图象上一点,AO的延长线交函数 ![]() (x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于
(x>0,k>0的常数)的图象于点C,点A关于y轴的对称点为A′,点C关于x轴的对称点为C′且点O、A′、C′在同一条直线上,连接CC′,交x轴于点B,连接AB,AA′,A′C′,若△ABC的面积等于6,则由线段AC,CC′,C′A′,A′A所围成的图形的面积等于
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列命题中,属于假命题的是( )
A. 三角形的内角和等于180°; B. 圆是轴对称图形,任何一条直径都是圆的对称轴;
C. 对顶角相等; D. 在同一平面内,垂直于同一条直线的两条直线相互平行.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小丽购买学习用品的收据如表,因污损导致部分数据无法识别,根据下表,解决下列问题:
(1)小丽买了自动铅笔、记号笔各几支?
(2)若小丽再次购买软皮笔记本和自动铅笔两种文具,共花费15元,则有哪几种不同的购买方案?
商品名 | 单价(元) | 数量(个) | 金额(元) |
签字笔 | 3 | 2 | 6 |
自动铅笔 | 1.5 | ● | ● |
记号笔 | 4 | ● | ● |
软皮笔记本 | ● | 2 | 9 |
圆规 | 3.5 | 1 | ● |
合计 | 8 | 28 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com