【题目】如图所示，在
中，
分别是
边上的点，且
，则
______．
【答案】
【解析】
在△ABC中，根据等边对等角得出∠B=∠C．在△BEP和△CFP中根据等边对等角和三角形内角和定理，∠EPB=∠FPC，等量代换得到∠BEP=∠FPC，根据三角形外角的性质得出∠B=∠EPF=50°，然后即可三角形内角和定理即可求出∠A的度数．
∵在△ABC中，AB=AC，
∴∠B=∠C．
∵BE=BP，
∴∠BEP=∠EPB，
同理，∠FPC=∠PFC．
∵∠B+2∠EPB=∠C+2∠FPC=180°，
∴∠EPB=∠FPC，
∴∠BEP=∠FPC．
∵∠B+∠BEP=∠EPC=∠EPF+∠FPC，
∴∠B=∠EPF=50°，
∴∠A=180°－2∠B=180°－2×50°=80°．
故答案为：80．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】小颖、小明、小亮在解方程
时，解法各不相同，请你回答下列问题：
（1）简要分析一下三位同学的解法是否正确．如果正确，他运用了哪种解一元二次方程的方法；如果错误，错误的原因是什么？你是否从中体会到解一元二次方程的数学思想是什么？
（2）请你选择一种你熟练的方法尝试解一元二次方程
．
由方程 因此 所以这个数是0或3 | 方程
|
即 或 所以这个数是0或3． |
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在矩形ABCD中，AB＝4，BC＝5，点E是边CD的中点，将△ADE沿AE折叠后得到△AFE．延长AF交边BC于点G，则CG为_____．
查看答案和解析>>
科目：初中数学 来源： 题型：
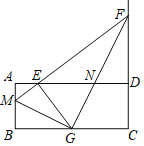
【题目】在矩形ABCD中，AB＝4，AD＝10，E是AD的一点，且AE＝2，M是AB上一点，射线ME交CD的延长线于点F，EG⊥ME交BC于点G，连接MG，FG，FG交AD于点N．
（1）当点M为AB中点时，则DF＝ ，FG＝ ．（直接写出答案）
（2）在整个运动过程中，
的值是否会变化，若不变，求出它的值；若变化，请说明理由．
（3）若△EGN为等腰三角形时，请求出所有满足条件的AM的长度．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
于
，连接
交
于点
,
．
（1）如图1，求证:
；
（2）如图2，
于点
，求证:
；
（3）如图3，点
在
的延长线上，
于点
交
于点
，连接
,
交的延长线于点
，连接
，当
的面积为
时， 求
的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，已知△ABC中，AB=BC，以AB为直径的⊙O交AC于点D，过D作DE⊥BC，垂足为E，连结OE，CD=
，∠ACB=30°．
（1）求证：DE是⊙O的切线；
（2）分别求AB，OE的长．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某商店购买60件A商品和30件B商品共用了1080元，购买50件A商品和20件B商品共用了880元．
（1）A、B两种商品的单价分别是多少元？
（2）已知该商店购买B商品的件数比购买A商品的件数的2倍少4件，如果需要购买A、B两种商品的总件数不少于32件，且该商店购买的A、B两种商品的总费用不超过296元，那么该商店有哪几种购买方案？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
