

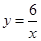 .
.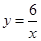 .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源:不详 题型:解答题
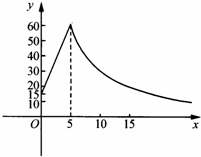
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
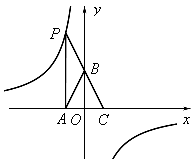
 图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=
图象上的点,PA垂直x轴于点A(-1,0),点C的坐标为(1,0),PC交y轴于点B,连结AB,已知AB=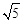 。
。
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
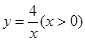 图象上的三个整点(即横、纵坐标均为整数的点),分别以这些点向横轴或纵轴作垂线段,由垂线段为边作出三个正方形,再以正方形的边长为直径作两个半圆,组成如图所示的阴影部分,则阴影部分的面积总和是 .(用含π的代数式表示)
图象上的三个整点(即横、纵坐标均为整数的点),分别以这些点向横轴或纵轴作垂线段,由垂线段为边作出三个正方形,再以正方形的边长为直径作两个半圆,组成如图所示的阴影部分,则阴影部分的面积总和是 .(用含π的代数式表示)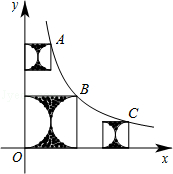
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
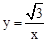 在第一象限内的图象经过OB边的中点C,则点B的坐标是
在第一象限内的图象经过OB边的中点C,则点B的坐标是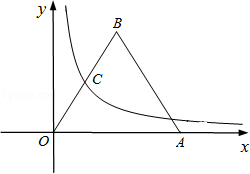
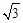 ) B.(
) B.(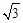 ,1) C.(2,
,1) C.(2,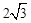 ) D,(
) D,(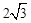 ,2)
,2)查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 与
与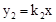 的图象相交于点A(1,2)和点B,当
的图象相交于点A(1,2)和点B,当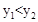 时,自变量x的取值范围是【 】
时,自变量x的取值范围是【 】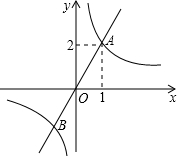
| A.x>1 | B.-1<x<0 |
| C.-1<x<0或x>1 | D.x<-1或0<x<1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com