
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;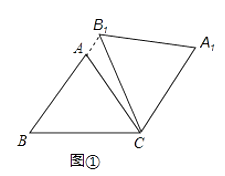
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.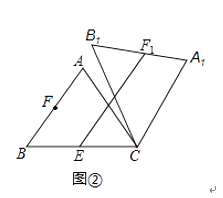
【答案】
(1)①证明:∵AB=AC,B1C=BC,
∴∠BB1C=∠B,∠B=∠ACB,
∵∠A1CB1=∠ACB(旋转角相等),
∴∠BB1C=∠A1CB1,
∴BB1∥CA1,
②过A作AF⊥BC于F,过C作CE⊥AB于E,
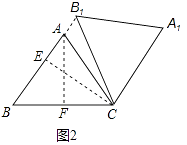
∵AB=AC,AF⊥BC,
∴BF=CF,
∵cos∠ABC=0.6,AB=5,
∴BF=3,
∴BC=6∴B1C=BC=6
∵CE⊥AB,
∴BE=B1E= ![]() ×6=
×6= ![]() ,
,
∴BB1= ![]() ,CE=
,CE= ![]() ,
,
∴AB1= ![]() ,
,
∴△AB1C的面积为: ![]() =
= ![]()
(2)如图3,
过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,EF1有最小值.
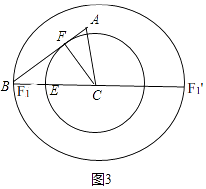
此时在Rt△BFC中,CF=4.8,
∴CF1=4.8,
∴EF1的最小值为4.8﹣3=1.8;
如图,以C为圆心BC为半径画圆交BC的延长线于F1',EF1'有最大值.
此时EF1'的最大值为EC+CF1'=3+6=9,
∴线段EF1的最大值与最小值的差为9﹣1.8=7.2.
【解析】(1)①根据旋转的性质和平行线的性质证明;②过A作AF⊥BC于F,过C作CE⊥AB于E,根据等腰三角形的性质和三角形的面积公式解答;(2)过C作CF⊥AB于F,以C为圆心CF为半径画圆交BC于F1,以C为圆心BC为半径画圆交BC于F1,得出最大和最小值解答即可。
【考点精析】认真审题,首先需要了解三角形的面积(三角形的面积=1/2×底×高),还要掌握等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角))的相关知识才是答题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
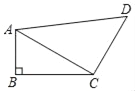
【题目】如图,四边形ABCD中,∠B=90°,∠ACB=30°,AB=2,CD=3,AD=5.
(1)求证:AC⊥CD;
(2)求四边形ABCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,MN,EF是两面互相平行的镜面,根据镜面反射规律,若一束光线AB照射到镜面MN上,反射光线为BC,则一定有∠1=∠2.试根据这一规律:
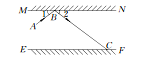
(1)利用直尺和量角器作出光线BC经镜面EF反射后的反射光线CD;
(2)试判断AB与CD的位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点分别表示两幢大楼所在的位置,直线a表示输水总管道,直线b表示输煤气总管道.现要在这两根总管道上分别设一个连接点,安装分管道将水和煤气输送到A,B两幢大楼,要求使铺设至两幢大楼的输水分管道和输煤气分管道的用料最短.图中,点A'是点A关于直线b的对称点,A'B分别交直线b,a于点C,D;点B'是点B关于直线a的对称点,B'A分别交直线b,a于点E,F.则符合要求的输水和输煤气分管道的连接点依次是
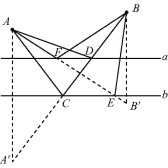
A. F和C B. F和E C. D和C D. D和E
查看答案和解析>>
科目:初中数学 来源: 题型:
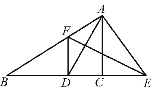
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线分别交AB于点F,交BC的延长线于点E.
求证:(1)∠EAD=∠EDA;
(2)DF∥AC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校对“学生在学校拿手机影响学习的情况”进行了调查,随机调查了部分学生,对此问题的看法分为三种情况:没有影响、影响不大、影响很大,并将调查结果绘制成如下不完整的统计表和扇形统计图,根据统计图表提供的信息,解答下列问题:
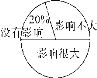
人数统计表如下:
看法 | 没有影响 | 影响不大 | 影响很大 |
学生人数(人) | 20 | 30 | a |
(1)统计表中的a= ;
(2)请根据表中的数据,谈谈你的看法(不少于2条)
查看答案和解析>>
科目:初中数学 来源: 题型:
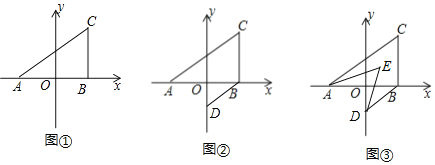
【题目】如图①,在平面直角坐标系中,点A、B在x轴上,AB⊥BC,AO=OB=2,BC=3
(1)写出点A、B、C的坐标.
(2)如图②,过点B作BD∥AC交y轴于点D,求∠CAB+∠BDO的大小.
(3)如图③,在图②中,作AE、DE分别平分∠CAB、∠ODB,求∠AED的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明到某服装商场进行社会调查,了解到该商场为了激励营业员的工作积极性,实行“月总收入=基本工资+计件奖金”的方法,并获得如下信息:
营业员A:月销售件数200件,月总收入3400元;
营业员B:月销售件数300件,月总收入3700元;
假设营业员的月基本工资为x元,销售每件服装奖动y元.
(1)求x和y的值;
(2)商场为了多销售服装,对顾客推荐一种购买方式:如果购买甲服装3件,乙服装2件,丙服袋1件共需390元:如果购买甲服装1件,乙服装2件,丙服装3件共需370元.某顾客想购买甲、乙、丙服装各一件共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等腰三角形,顶角∠BAC=α(α<60°),D是BC边上的一点,连接AD,线段AD绕点A顺时针旋转α到AE,过点E作BC的平行线,交AB于点F,连接DE,BE,DF. 
(1)求证:BE=CD;
(2)若AD⊥BC,试判断四边形BDFE的形状,并给出证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com