
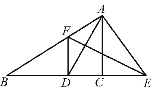
【题目】如图,在△ABC中,AD是∠BAC的平分线,AD的垂直平分线分别交AB于点F,交BC的延长线于点E.
求证:(1)∠EAD=∠EDA;
(2)DF∥AC.
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+3x交x轴正半轴于点A(6,0),顶点为M,对称轴MB交x轴于点B,过点C(2,0)作射线CD交MB于点D(D在x轴上方),OE∥CD交MB于点E,EF∥x轴交CD于点F,作直线MF.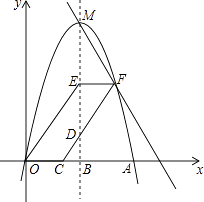
(1)求a的值及M的坐标;
(2)当BD为何值时,点F恰好落在该抛物线上?
(3)当∠DCB=45°时:
①求直线MF的解析式;
②延长OE交FM于点G,四边形DEGF和四边形OEDC的面积分别记为S1、S2 , 则S1:S2的值为(直接写答案)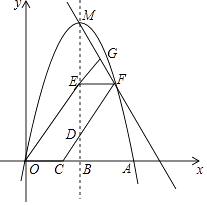
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中有一直角三角形AOB,O为坐标原点,OA=1,tan∠BAO=3,将此三角形绕原点O逆时针旋转90°,得到△DOC,抛物线y=ax2+bx+c经过点A,B,C.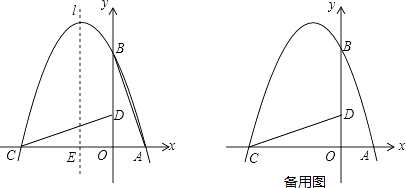
(1)求抛物线的解析式;
(2)若点P是第二象限内抛物线上的动点,其横坐标为t,
①设抛物线对称轴l与x轴交于一点E,连接PE,交CD于F,求出当△CEF与△COD相似时,点P的坐标;
②是否存在一点P,使△PCD的面积最大?若存在,求出△PCD的面积的最大值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=5,cos∠ABC=0.6,将△ABC绕点C顺时针旋转,得到△A1B1C.
(1)如图1,当点B1在线段BA延长线上时.①求证:BB1∥CA1;②求△AB1C的面积;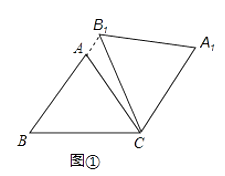
(2)如图2,点E是BC边的中点,点F为线段AB上的动点,在△ABC绕点C顺时针旋转过程中,点F的对应点是F1 , 求线段EF1长度的最大值与最小值的差.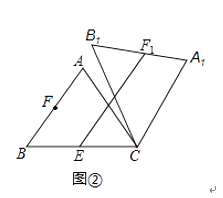
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“二广”高速在益阳境内的建设正在紧张地进行,现有大量的沙石需要运输.“益安”车队有载重量为8吨、10吨的卡车共12辆,全部车辆运输一次能运输110吨沙石.
(1)求“益安”车队载重量为8吨、10吨的卡车各有多少辆?
(2)随着工程的进展,“益安”车队需要一次运输沙石165吨以上,为了完成任务,准备新增购这两种卡车共6辆,车队有多少种购买方案,请你一一写出.
查看答案和解析>>
科目:初中数学 来源: 题型:
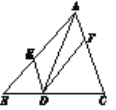
【题目】如图,在△ABC中,点D、E、F分别在边BC、AB、CA上,且DE∥CA,DF∥BA.则下列说法:
①四边形AEDF是平行四边形;
②如果∠BAC=90°,那么四边形AEDF是矩形;
③如果AD平分∠BAC,那么四边形AEDF是菱形;
④如果∠BAC=90°,AD平分∠BAC,那么四边形AEDF是正方形.
其中正确的是______(只填写序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】利用完全平方公式进行因式分解,解答下列问题:
![]() 因式分解:
因式分解:![]() .
.
![]() 填空: ①当
填空: ①当![]() 时,代数式
时,代数式![]() _ .
_ .
②当![]() _ 时,代数式
_ 时,代数式![]() .
.
③代数式![]() 的最小值是_ .
的最小值是_ .
![]() 拓展与应用:求代数式
拓展与应用:求代数式![]() 的最小值.
的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com